Алгоритми заповнення областей

Для заповнення областей, обмежених замкнутою лінією, застосовуються два основних підходи: затравочное заповнення й растрове розгорнення.

Методи першого типу виходять із того, що задано деяку крапку (запал) усередині контуру й заданий критерій приналежності крапки границі області (наприклад, заданий колір границі). В алгоритмах шукають крапки, сусідні із затравочной і розташовані усередині контуру. Якщо виявлено сусідню крапку, що належить внутрішньої області контуру, то вона стає затравочной і пошук триває рекурсивно.

Методи растрового розгорнення засновані на скануванні рядків растра й визначенні, чи лежить крапка усередині заданого контуру області. Сканування здійснюється найчастіше "зверху долілиць", а алгоритм визначення приналежності крапки заданої області залежить від виду її границі.

Спочатку розглянемо простий алгоритм заповнення із запалом з використанням стека. Під стеком у цьому випадку ми будемо розуміти масив, у який можна послідовно поміщати значення й послідовно витягати, причому витягають елементи не в порядку надходження, а навпаки: за принципом "першим прийшов - останнім пішов" ("first in - last out"). Алгоритм заповнення виглядає в такий спосіб:

Помістити затравочный пиксель у стек

Поки стік не порожній:

Витягти пиксель зі стека

Инициализировать пиксель

Для кожного із чотирьох сусідніх пикселей:

Перевірити, чи є він граничним і чи був він инициализирован

Якщо ні, то помістити пиксель у стек

Алгоритм можна модифікувати таким чином, що сусідніми будуть уважатися вісім пикселей (додаються елементи, розташовані в діагональному напрямку).

Методи растрового розгорнення розглянемо спочатку в застосуванні до заповнення багатокутників. Найпростіший метод побудови полягає в тому, щоб для кожного пикселя растра перевірити його приналежність внутрішності багатокутника. Але такий перебір занадто неекономічний, оскільки фігура може займати лише незначну частину екрана, а геометричний пошук - завдання трудомістка, сполучена з довгими обчисленнями. Алгоритм стане більше ефективним, якщо попередньо виявити мінімальний прямокутник, у який занурений контур багатокутника, але й этого може виявитися недостатньо.

У випадку, коли багатокутник, що обмежує область, заданий списком вершин і ребер (ребро визначається як пара вершин), можна запропонувати ще більш ощадливий метод. Для кожної сканирующей рядки визначаються крапки перетинання з ребрами багатогранника, які потім упорядковуються по координаті 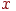. Визначення того, який інтервал між парами перетинань є внутрішній для багатогранника, а який ні, є досить простим логічним завданням. При цьому якщо сканирующая рядок проходить через вершину багатогранника, те це перетинання повинне бути враховане двічі у випадку, коли вершина є крапкою локального мінімуму або максимуму. Для пошуку перетинань сканирующей рядка з ребрами можна використовувати алгоритм Брезенхема побудови растрового образа відрізка.

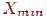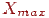На закінчення як приклад приведемо алгоритм зафарбування внутрішньої області трикутника, заснований на складанні повного впорядкованого списку всіх відрізків, що становлять цей трикутник. Для запису горизонтальних координат кінців цих відрізків будемо використовувати два масиви й розмірністю, рівної числу пикселей растра по вертикалі (мал. 10.11).

Побудова починається з ініціалізації масивів 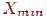і 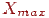: масив 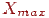заповнюється нулями, а масив 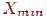- числом 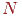, рівним числу пикселей растра по горизонталі. Потім визначаємо значення 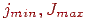, що обмежують трикутник у вертикальному напрямку. Тепер, використовуючи модифікований алгоритм Брезенхема, занесемо границі відрізків у масив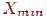и й 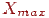. Для цього щораз при переході до чергового пикселю при формуванні відрізка замість його ініціалізації будемо порівнювати його координату 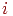із умістом 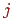-й осередку масивів. Якщо 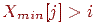, то записуємо координату 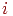в масив 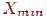. Аналогічно за умови 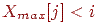координату 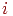записуємо в масив .

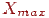Якщо тепер послідовно застосувати алгоритм Брезенхема до всім трьох сторонам трикутника, то ми одержимо потрібним образом заповнені масиви границь. Залишається тільки проинициализировать пиксели усередині відрізків .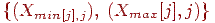

Цей алгоритм можна легко поширити на випадок довільного опуклого багатокутника.

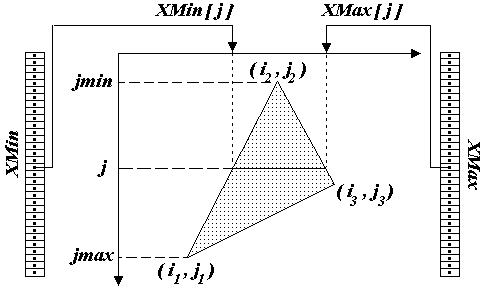
Рис. 10.11. Схема побудови растрового розгорнення трикутника

Питання й вправи

1. Що таке розкладання в растр?

2. Яка математична основа растрового розкладання в алгоритмі Брезенхема?

3. За яким критерієм инициализируется пиксель у цьому алгоритмі?

4. Чим відрізняються галузі алгоритму при кутах нахилу <45° і >45°?

5. Яку частину окружності досить побудувати, щоб потім шляхом відбиттів одержати окружність цілком?

6. Яку частину еліпса досить побудувати, щоб потім шляхом відбиттів одержати еліпс цілком?

7. Назвіть два типи алгоритмів заповнення областей.

8. Яка структура даних використовується в алгоритмах із запалом?

9. Які дані використовуються при побудові растрового розгорнення трикутника?