Зафарбування методом Гуро

Один зі способів усунення дискретності интенсивностей зафарбовування був запропонований Гуро. Його метод полягає в тім, що використовуються не нормалі до плоских граней, а нормалі до аппроксимируемой поверхні, побудовані у вершинах багатогранника. Після цього обчислюються інтенсивності у вершинах, а потім у всіх внутрішніх крапках багатокутника виконується билинейная інтерполяція інтенсивності.

Метод сполучається з алгоритмом порядкового сканування. Після того як грань відображена на площину зображення, для кожної сканирующей рядки визначаються її крапки перетинання з ребрами. У цих крапках інтенсивність обчислюється за допомогою лінійної інтерполяції интенсивностей у вершинах ребра. Потім для всіх внутрішніх крапок багатокутника, що лежать на сканирующей рядку, також обчислюється інтенсивність методом лінійної інтерполяції двох отриманих значень. На мал. 11.5 показаний плоский багатокутник з обчисленими значеннями интенсивностей у вершинах.

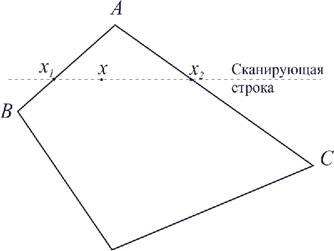
Рис. 11.5. Інтерполяція інтенсивності

Нехай 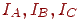- інтенсивності у вершинах 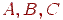, 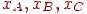- горизонтальні координати цих крапок. Тоді в крапках перетинання сканирующей рядка з ребрами багатокутника інтенсивності можна обчислити по формулах інтерполяції:

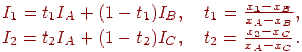
(11.7)

Після цього інтенсивність у крапці 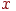одержуємо шляхом інтерполяції значень на кінцях відрізка:

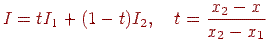
(11.8)

До недоліків методу Гуро варто віднести те, що він добре працює тільки з дифузійною моделлю відбиття. Форма відблисків на поверхні і їхнє розташування не можуть бути адекватно відтворені при інтерполяції на багатокутниках. Крім того, є проблема побудови нормалей до поверхні. В алгоритмі Гуро нормаль у вершині багатогранника обчислюється шляхом усереднення нормалей до граней, пов'язаним із цією вершиною. Така побудова сильно залежить від характеру розбивки.