Проста модель висвітлення

Об'єкти навколишнього простору стають видимими для ока завдяки світловій енергії, що може випромінюватися поверхнею предмета, відбиватися або проходити крізь неї. У свою чергу, відбиття світла від поверхні залежить від фізичних властивостей матеріалу, з якого вона виготовлена, а також від характеру й розташування джерела світла. Яскравість (або інтенсивність) висвітлення залежить від енергії світлового потоку, що обумовлює, в- перших, потужністю джерела світла, а по-друге, що відбивають і пропускають властивостями об'єкта.

Спочатку ми розглянемо модель висвітлення, що враховує тільки відбиття. Властивості відбитого світла залежать головним чином від напрямку променів і характеристик поверхні, що відбиває.

Відбиття може бути двох видів: дифузійне й дзеркальне. Перше з них виникає в ситуації, коли світло як би проникає під поверхню об'єкта, поглинається, а потім рівномірно випромінюється у всіх напрямках. Поверхня в цьому випадку розглядається як ідеальний розсіювач. При цьому виникає ефект матового світла, а видима освітленість тої або іншої ділянки поверхні не залежить від положення спостерігача. Дзеркальне відбиття, навпаки, походить від зовнішньої поверхні, інтенсивність його неоднорідна, тому видимий максимум освітленості залежить від положення ока спостерігача.

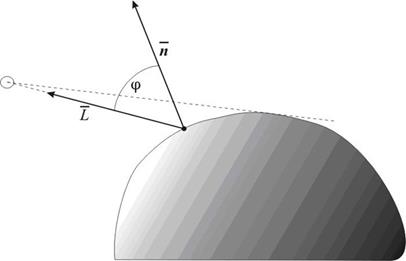
Рис. 11.2. Висвітлення крапковим джерелом

Світло крапкового джерела відбивається від поверхні розсіювача за законом Ламберта: інтенсивність відбиття пропорційна косинусу кута між зовнішньою нормаллю до поверхні й напрямком до джерела світла (мал. 11.2). Якщо 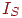- інтенсивність джерела світла, 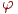- кут між вектором зовнішньої нормалі до поверхні й напрямком до джерела світла, то інтенсивність відбитого світла визначається формулою

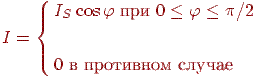
(11.1)

При такому розрахунку інтенсивності вийде дуже контрастна картина, тому що ділянки поверхні, на які промені від джерела не попадають прямо, залишаться абсолютно чорними. Для підвищення реалістичності необхідно враховувати розсіювання світла в навколишньому просторі. Тому вводиться фонова освітленість, що залежить від інтенсивності розсіяного світла 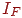, і інтенсивність відбитого світла визначається вираженням

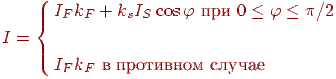
(11.2)

де 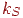- коефіцієнт дифузійного відбиття розсіяного світла, 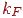- коефіцієнт дифузійного відбиття падаючого світла, .

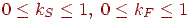В описаній моделі поки ніяк не враховувалася далекість джерела світла від поверхні, тому по освітленості двох об'єктів не можна судити про їхнє взаємне розташування в просторі. Якщо ми хочемо одержати перспективне зображення, то необхідно включити загасання інтенсивності з відстанню. Звичайно інтенсивність світла обернено пропорційна квадрату відстані від джерела. Як відстань до джерела у випадку перспективного перетворення можна взяти відстань до центра проекції, і якщо він досить вилучений, то зображення буде досить адекватним. Але якщо цей центр розташований близько до об'єкта, то квадрат відстані міняється дуже швидко, і в цьому випадку краще використовувати лінійне загасання. У цьому випадку інтенсивність відбитого світла від безпосередньо освітлених ділянок поверхні буде задаватися формулою

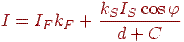
(11.3)

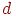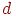де - відстань до центра проекції, а - довільна постійна. Якщо центр проекції перебуває на нескінченності, тобто при паралельному проектуванні, то в якості можна взяти відстань до об'єкта, найбільш близького до спостерігача.

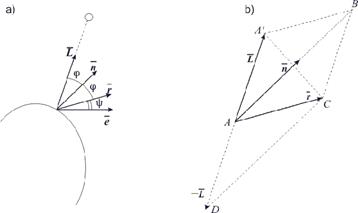
Рис. 11.3. Дзеркальне відбиття

На відміну від дифузійного, дзеркальне відбиття є спрямованим. Ідеальне дзеркало відбиває промені за принципом "відбитий і падаючий промені лежать в одній площині, причому кут падіння дорівнює куту відбиття" (мається на увазі кут між напрямком лучачи й нормаллю до поверхні). Якщо поверхня не ідеально дзеркальна, то промені відбиваються в різних напрямках, але з різною інтенсивністю, а функція зміни інтенсивності має чітко виражений максимум. Оскільки фізичні властивості дзеркального відбиття досить складні, то в комп'ютерній графіці використовується емпірична модель Фонга. Суть її полягає в тім, що для ока спостерігача інтенсивність дзеркально відбитого лучачи залежить від кута між ідеально відбитим променем і напрямком до спостерігача (мал. 11.3a). Крім того, оскільки дзеркальне відбиття залежить ще й від довжини хвилі, це також будемо враховувати у формулі для обчислення інтенсивності. Модель Фонга описується співвідношенням

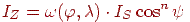
(11.4)

де 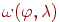- функція відбиття, 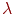- довжина хвилі. Ступінь, у яку зводиться косинус кута, впливає на розміри світлового відблиску, спостережуваного глядачем. Графіки цієї функції наведені на мал. 11.4, і вони саме є характерними кривими поводження функції зміни інтенсивності залежно від властивостей поверхні.

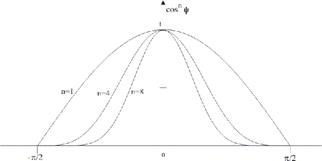
Рис. 11.4. Дзеркальне відбиття

Тепер модель освітленості, що враховує дзеркальне й дифузійне відбиття, можна описати формулою

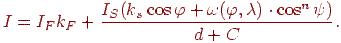
(11.5)

Використовуючи одиничні вектори 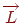(напрямок до джерела) і 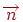(зовнішня нормаль), косинус кута 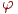можна обчислити через скалярний добуток: 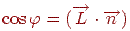. Для розрахунку інтенсивності дзеркального відбиття спочатку треба визначити відбитий вектор 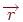. З мал. 11.3b видно, що 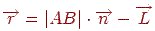. З іншої сторони 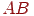є діагоналлю ромба 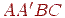, тому 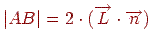. З огляду на всі ці співвідношення, одержуємо формулу

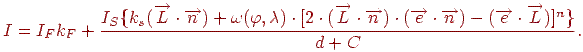
(11.6)

В алгоритмах зафарбовування з використанням колірних моделей інтенсивність розраховується для кожного з базових квітів, оскільки зміна інтенсивності при дзеркальному відбитті залежить від довжини хвилі.