Преобразование Фурье от последовательности

Пусть имеется сигнал 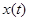, и выбран шаг дискретизации 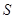. Функция заменяется последовательностью .

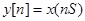Определение.Преобразованием Фурье от последовательности называется функция

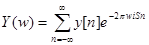(1)

Отметим, что функция 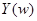является периодической. Часто ради простоты обозначений полагают 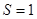, и в этом случае период функции равен 1. Это принципиальное различие между преобразованиями Фурье от функции и последовательности. В то же время, оба преобразования тесно связаны. Положим 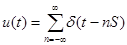. Тогда

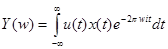, (2)

то есть является преобразованием Фурье от произведения двух функций, из которых одна - обобщенная функция. Согласно общей теории, преобразование Фурье от произведения двух функций равно свертке образов сомножителей. Здесь мы отступаем от строгого изложения, поскольку уже справедливость (2) требует обоснования. Для упрощения обозначений положим 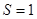. Найдем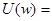 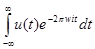. Снова положим =

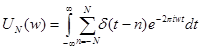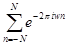. Обратим внимание на то, что это периодическая функция с периодом 1, представленная суммой геометрической прогрессии. Имеем:

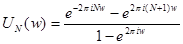. Умножим числитель и знаменатель на 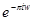. Получим 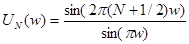В окрестности 0 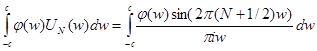. стремятся при 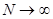к

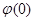. Таким образом, в окрестности 0 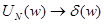. В силу периодичности, имеем окончательный результат: 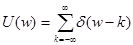. Для произвольного 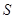можем написать формулу

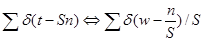(3)