Теорема Котельникова-Шеннона
Эта теорема уточняет результат предыдущего пункта.
Если исходный сигнал имеет ограниченный спектр и выполнено условие (5), то непрерывный сигнал можно восстановить по дискретному.
Доказательство. Пусть спектр сигнала находится в интервале  . Выберем произвольное
. Выберем произвольное 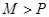 . Тогда
. Тогда 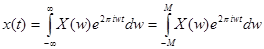 . Функцию, заданную на конечном интервале, можно разложить в ряд Фурье:
. Функцию, заданную на конечном интервале, можно разложить в ряд Фурье: 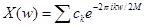 , где
, где 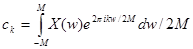 . Отсюда следует, что
. Отсюда следует, что 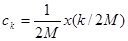 . Теперь
. Теперь 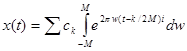 . Положив
. Положив 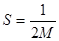 . Получим
. Получим
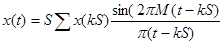 . (6)
. (6)
Замечание. Обратим внимание, что в (5) должно выполняться строгое неравенство, если мы хотим, чтобы утверждение оставалось верным и для сигналов с преобразованием Фурье в виде обобщенной функции. В качестве примера рассмотрим  . Спектр сигнала сосредоточен на интервале
. Спектр сигнала сосредоточен на интервале 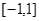 . Положим
. Положим 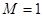 , тогда
, тогда 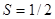 , но последовательность
, но последовательность 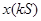 оказывается нулевой. То есть непрерывный сигнал не удается восстановить по дискретным значениям. Если же
оказывается нулевой. То есть непрерывный сигнал не удается восстановить по дискретным значениям. Если же 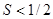 , то можно воспользоваться формулой (6).
, то можно воспользоваться формулой (6).
 Лекция 4. Дискретное преобразование Фурье (ДПФ)
Лекция 4. Дискретное преобразование Фурье (ДПФ)
В данной лекции установим свойства дискретного преобразования Фурье аналогичные свойствам непрерывного преобразования. Как обычно, преобразования типа почленного интегрирования ряда, перестановки порядка суммирования и т.п будут проводится без какого-либо обоснования. Предполагается, что соответствующие функции обладают необходимыми свойствами.
Основное определение: 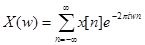
Дата добавления: 2015-05-13; просмотров: 946;
