Лекция 3 Восстановление дискретного сигнала
Цифровая обработка сигналов. Основные понятия
Введение
В настоящее время методы цифровой обработки сигналов, digital signal processing (DSP) находят все более широкое применение, вытесняя постепенно методы, основанные на аналоговой обработке. В данном курсе рассматриваются основы теории, и наиболее употребляемые алгоритмы обработки.
При работе над данным конспектом автор пользовался следующими источниками
1. Р.Отнес, Л.Энокон. Прикладной анализ временных рядов. М.:Мир, 1982.
2. A.Oppenheim, R.Schafer. Discrete-time signal processing. Prentice-Hall, 1989.
Кроме того, при изложении вопросов, связанных с Wavelet теорией использованы статьи, о которых будет сказано в соответствующем месте.
Постановка задачи.
|
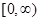 . При переходе к оцифровке происходит следующая операция. Выбирается шаг дискретизации
. При переходе к оцифровке происходит следующая операция. Выбирается шаг дискретизации 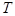 , и вместо исходного сигнала получается последовательность
, и вместо исходного сигнала получается последовательность 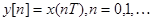 . Далее, выбирается формат оцифровки r. Обычно он бывает кратным 8, хотя это не обязательно. Предположим, что существует такое число М, что выполнены неравенства:
. Далее, выбирается формат оцифровки r. Обычно он бывает кратным 8, хотя это не обязательно. Предположим, что существует такое число М, что выполнены неравенства: 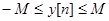 для всех n. Интервал [-M,M] разбивается на
для всех n. Интервал [-M,M] разбивается на 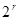
 частей. После этого каждое значение
частей. После этого каждое значение 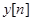 заменяется номером интервала, в который попало соответствующее значение. В результате последовательность
заменяется номером интервала, в который попало соответствующее значение. В результате последовательность 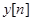 заменяется новой последовательностью
заменяется новой последовательностью 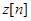 , но теперь каждый член новой последовательности принимает значения из интервала
, но теперь каждый член новой последовательности принимает значения из интервала  . При желании вместо указанного представления можно перейти к представлению сигнала целыми числами со знаком.
. При желании вместо указанного представления можно перейти к представлению сигнала целыми числами со знаком.
На каждом из упомянутых шагов происходит огрубление сигнала. Первая задача цифровой обработки заключается в оценке искажения исходного сигнала. Дальнейшая обработка состоит в извлечении из полученного сигнала нужной информации и подавлении шумов. Это осуществляется с помощью цифровой фильтрации. Даже оцифрованный сигнал занимает много места, и следующий шаг обработки заключается в сжатии сигнала. Обычно имеется в виду сжатие с потерей информации. Здесь важно установить критерии допустимой потери информации. В зависимости от выбранного критерия выбирается способ сжатия. Хотя последовательность бесконечна, в реальных условиях мы имеем дело лишь с конечными последовательностями. В этой связи нужна оценка потерь, связанных с усечением последовательностей.
Преобразование Фурье
Важнейшей характеристикой исходного сигнала является его преобразование Фурье. Если исходный сигнал задан функцией 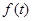 , заданной на всей вещественной оси, то его преобразование Фурье задается формулой
, заданной на всей вещественной оси, то его преобразование Фурье задается формулой
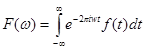 (1)
(1)
Функция 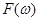 или ее модуль трактуется как интенсивность исходного сигнала на частоте
или ее модуль трактуется как интенсивность исходного сигнала на частоте 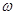 . Обратное преобразование задается аналогичной формулой:
. Обратное преобразование задается аналогичной формулой:
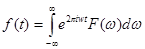 (2)
(2)
Справедливость указанных формул возможна лишь при определенных ограничениях на исходные функции. В зависимости от наложенных ограничений данным формулам придают различный смысл. Мы не будем уточнять данное обстоятельство, предполагая, что все выполняемые операции типа изменения порядка интегрирования законны. Однако в любом случае при обычном понимании интегрирования необходимым условием является убывание функций на бесконечности. В реальных условиях это ограничение не имеет места, поэтому предварительно нужно ознакомиться со специальным математическим аппаратом, позволяющим в некоторых случаях обойти данное ограничение.
Прежде, чем переходить к изложению этого аппарата, напомним основные свойства преобразования Фурье. Для краткости связь между функцией и ее преобразованием Фурье будем обозначать так: 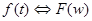 .
.
Если 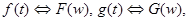 то
то 
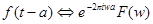
Сверткой двух функций называется функция 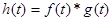 , заданная формулой:
, заданная формулой:  . Имеет место соотношение
. Имеет место соотношение 
Двойственное соотношение имеет вид 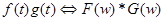 .
.
Вообще говоря, не предполагается, что функция 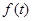 - вещественная. Если же это так, то
- вещественная. Если же это так, то 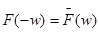
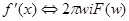 . Эта формула получается формальным дифференцированием под знаком интеграла в (2).
. Эта формула получается формальным дифференцированием под знаком интеграла в (2).
Обобщенные функции
Как уже отмечалось, для того, чтобы в обычном смысле существовало преобразование Фурье от функции, необходимо ее убывание на бесконечности. Очевидно, что это не выполнено для стационарного сигнала. Для того, чтобы иметь возможность работать с преобразованием Фурье и от таких функций нужен вспомогательный аппарат.
Обозначим через 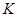 множество бесконечно дифференцируемых функций с компактным носителем. По определению, последовательность
множество бесконечно дифференцируемых функций с компактным носителем. По определению, последовательность  , если все эти функции имеют общий компактный носитель, принадлежат
, если все эти функции имеют общий компактный носитель, принадлежат 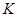 и в каждой точке имеет место обычная сходимость. Функционал это отображение
и в каждой точке имеет место обычная сходимость. Функционал это отображение 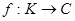 , причем
, причем 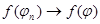 . Если
. Если 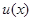 - интегрируемая функция, то ей соответствует функционал
- интегрируемая функция, то ей соответствует функционал  . Однако существуют функционалы, не представимые в указанной форме. Например,
. Однако существуют функционалы, не представимые в указанной форме. Например, 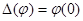 . Этот функционал записывают в форме
. Этот функционал записывают в форме 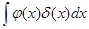 . Наряду с указанным функционалом определяют функционалы
. Наряду с указанным функционалом определяют функционалы 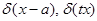 , исходя из формального правила замены переменных в интеграле. Хотя этот функционал нельзя представить с помощью обычной функции, можно ввести
, исходя из формального правила замены переменных в интеграле. Хотя этот функционал нельзя представить с помощью обычной функции, можно ввести 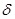 -образную последовательность. Положим
-образную последовательность. Положим 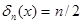 при
при 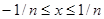 и 0 в остальных точках. Интеграл от нее равен 1. При больших
и 0 в остальных точках. Интеграл от нее равен 1. При больших 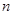 функция
функция 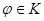 представима в виде
представима в виде  при
при 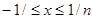 , поэтому
, поэтому 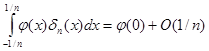 (второе слагаемое исчезает в силу симметричности).
(второе слагаемое исчезает в силу симметричности).
Лемма. Пусть 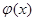 имеет интегрируемую производную. Тогда
имеет интегрируемую производную. Тогда 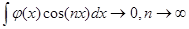
Доказательство проводится интегрированием по частям. Аналогичное утверждение справедливо и для  .
.
Задача 1. Доказать, что 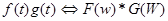
Лекция 2. Преобразование Фурье и обобщенные функции
Вспомогательные утверждения
Лемма. Справедлива формула
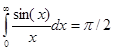 (1)
(1)
Доказательство. Хотя формула (1) хорошо известна, мы приведем ее доказательство, поскольку она является основой многих дальнейших выкладок. Рассмотрим контур, изображенный на рис.1
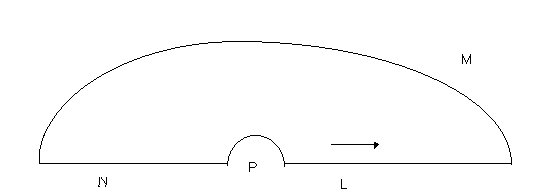 Рис. 1. Контур интегрирования
Рис. 1. Контур интегрирования
|
и интеграл по контуру в указанном направлении от аналитической функции 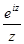 . Имеем
. Имеем 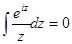 , поскольку у функции нет особенностей внутри области интегрирования. Здесь контур
, поскольку у функции нет особенностей внутри области интегрирования. Здесь контур 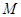 - дуга окружности радиуса
- дуга окружности радиуса 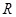 , а контур
, а контур 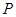 - дуга окружности радиуса
- дуга окружности радиуса 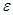 . Обе дуги имеют центр в начале координат. За исключением крайних точек, на контуре
. Обе дуги имеют центр в начале координат. За исключением крайних точек, на контуре 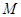 выполнено неравенство
выполнено неравенство 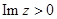 , поэтому с ростом
, поэтому с ростом 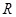 интеграл по этому контуру стремится к 0. Интегралы по контурам
интеграл по этому контуру стремится к 0. Интегралы по контурам  в сумме дают
в сумме дают 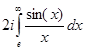 . Найдем теперь интеграл по контуру
. Найдем теперь интеграл по контуру 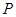 . Сделаем замену
. Сделаем замену 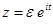 . В результате интеграл по этому контуру примет вид
. В результате интеграл по этому контуру примет вид 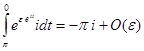 . Последняя оценка получена в результате разложения подынтегральной функции в ряд. Устремляя
. Последняя оценка получена в результате разложения подынтегральной функции в ряд. Устремляя 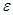 к 0, завершаем доказательство.
к 0, завершаем доказательство.
Следствие 1.

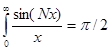
при любом 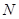 .
.
Доказательство проводится путем замены переменной
Следствие 2
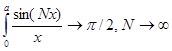 .
.
Для любого 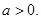
Доказательство. 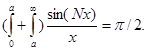 . Второе слагаемое стремится к 0 когда
. Второе слагаемое стремится к 0 когда 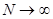 .
.
Из соображений симметрии вытекает формула
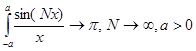 (2)
(2)
Пример отыскания обобщенных функций
Под обобщенной функцией понимается непрерывный функционал. Примером такой функции является 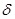 -функция.
-функция.
Предложение 1.  .
.
Доказательство. Очевидно, что обычное преобразование Фурье от 1 не существует. Положим 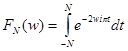 . Не существует обычного предела у этой функции при
. Не существует обычного предела у этой функции при 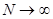 . Найдем функционал
. Найдем функционал 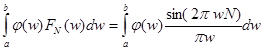 . Если 0 не попадает в интервал интегрирования, подынтегральная функция не имеет особенностей, и весь интеграл стремится к 0. В противном случае, интеграл стремится к
. Если 0 не попадает в интервал интегрирования, подынтегральная функция не имеет особенностей, и весь интеграл стремится к 0. В противном случае, интеграл стремится к 
 , где
, где 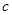 произвольное малое положительное число. Второе слагаемое исчезает в силу симметричности, и при
произвольное малое положительное число. Второе слагаемое исчезает в силу симметричности, и при 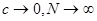 получаем, используя (2), конечный результат.
получаем, используя (2), конечный результат.
Следствие 3. 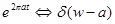 . Доказательство. Формально утверждение есть следствие общего правила:
. Доказательство. Формально утверждение есть следствие общего правила: 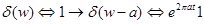 , но фактически надо доказать, что это правило распространяется и на обобщенные функции. Проще всего, дать прямое доказательство.
, но фактически надо доказать, что это правило распространяется и на обобщенные функции. Проще всего, дать прямое доказательство.
Производные от обобщенных функций
Производная определяется путем формального применения интегрирования по частям с учетом компактности носителя функций из 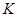 :
: 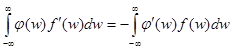 . В качестве примера рассмотрим обобщенную функцию
. В качестве примера рассмотрим обобщенную функцию 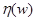 , заданную равенством:
, заданную равенством: 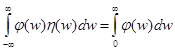 и найдем производную от нее. Имеем
и найдем производную от нее. Имеем 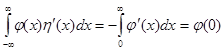 . Это означает, что
. Это означает, что 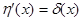 .
.
Замечание.Следует быть очень осторожным применяя к обобщенным функциям формулы, связывающие производную от функции и ее преобразование Фурье. В качестве примера рассмотрим отыскание преобразование Фурье от  . Действуя формально, можем получить:
. Действуя формально, можем получить: 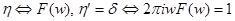 , откуда
, откуда 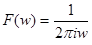 . Теперь, исходя из определения, найдем правильный ответ. Положим
. Теперь, исходя из определения, найдем правильный ответ. Положим 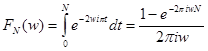 и подсчитаем
и подсчитаем 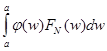 . Если точка 0 не входит в интервал интегрирования, то интеграл стремится к
. Если точка 0 не входит в интервал интегрирования, то интеграл стремится к 
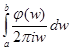 , то есть ожидаемый результат. Если же точка 0 принадлежит интервалу интегрирования, то наряду с указанным слагаемым появится еще одно.
, то есть ожидаемый результат. Если же точка 0 принадлежит интервалу интегрирования, то наряду с указанным слагаемым появится еще одно. 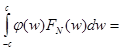
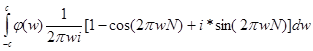
Второе слагаемое исчезает в силу симметрии, а из третьего слагаемого получаем 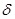 -функцию. Окончательный результат выглядит так:
-функцию. Окончательный результат выглядит так: 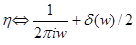 . Отметим, что отсюда получается правильный результат для преобразования Фурье от
. Отметим, что отсюда получается правильный результат для преобразования Фурье от 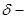 функции, поскольку
функции, поскольку 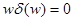 .
.
Замечание. Интеграл 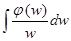 существует в смысле главного значения для функции из
существует в смысле главного значения для функции из 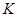 . Это означает существование соответствующего функционала.
. Это означает существование соответствующего функционала.
Задача 2. Дать строгое доказательство утверждения


Лекция 3 Восстановление дискретного сигнала
Наша цель - найти необходимые условия, при которых сигнал может быть восстановлен по дискретной выборке
Прежде всего, отметим часто часто используемый факт: 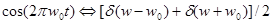
Дата добавления: 2015-05-13; просмотров: 2147;

