Пример вычисления ДПФ
Ранее было подсчитано ДПФ от единичной последовательности. В реальных условиях полагают, что в отрицательные моменты времени сигнал отсутствует. В этой связи интересно найти ДПФ от дискретного аналога функции 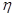 .
.
Предложение. 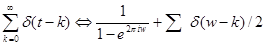
Доказательство. Положим 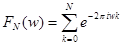 =
= 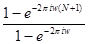 . Теперь
. Теперь
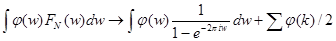
Задача 3. Доказать, что 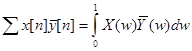
Линейные инвариантные системы.
Рассматриваются последовательности 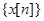 . Очевидным образом определяются сумма последовательностей и произведение на число. В результате сдвига получается новая последовательность
. Очевидным образом определяются сумма последовательностей и произведение на число. В результате сдвига получается новая последовательность 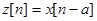 . Дальнейшее работа с последовательностью, полученной в результате дискретизации, заключается в преобразовании с помощью различных устройств.
. Дальнейшее работа с последовательностью, полученной в результате дискретизации, заключается в преобразовании с помощью различных устройств.
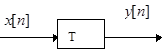
|
Система 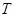 осуществляет это преобразование:
осуществляет это преобразование: 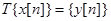 .. отметим, что выходная последовательность является функцией от всей входной последовательности, то есть каждый член входной последовательности зависит, вообще говоря, от всех членов входной последовательности.
.. отметим, что выходная последовательность является функцией от всей входной последовательности, то есть каждый член входной последовательности зависит, вообще говоря, от всех членов входной последовательности.
Определение. Система 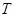 называется инвариантной, если
называется инвариантной, если 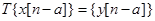 для любого
для любого 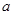 .
.
Примеры.
1. Точечные системы: 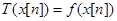 , где
, где 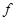 произвольная функция ,- инвариантная система..
произвольная функция ,- инвариантная система..
2. 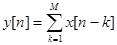 для произвольного фиксированного
для произвольного фиксированного 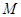 - инвариантная система
- инвариантная система
3. 
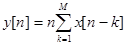 не будет инвариантной. Действительно, пусть
не будет инвариантной. Действительно, пусть 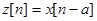 . Согласно определению
. Согласно определению 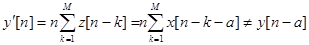
Определение. Система называется линейной инвариантной (ЛИС), если она линейна и инвариантна.
Преобразование в примере 2 осуществляется ЛИС.
Лекция 5. Цифровые фильтры. Основные понятия
Цифровые фильтры являются частным случаем линейных инвариантных систем. Существенное ограничение связано с физической реализуемостью системы.
Определение. Система называется физически реализуемой, если сигнал на выходе в момент времени t зависит от входных сигналов в моменты времени 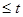 .
.
Пусть имеется ЛИС 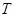 . Рассмотрим сосредоточенную в одной точке последовательность
. Рассмотрим сосредоточенную в одной точке последовательность 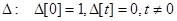 . Пусть
. Пусть 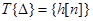 , а по определению
, а по определению 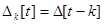 . Для произвольной последовательности
. Для произвольной последовательности 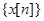 справедливо разложение
справедливо разложение 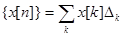 . В силу линейности
. В силу линейности 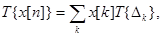 а в силу инвариантности
а в силу инвариантности 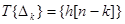 . Окончательно, если
. Окончательно, если 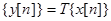 , то
, то
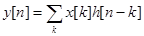 (1)
(1)
Другими словами, реакция на любую последовательность получается с помощью свертки этой последовательности и последовательности 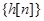 , называемой импульсной реакцией, или функцией отклика.
, называемой импульсной реакцией, или функцией отклика.

|
Если имеются две последовательно соединенных ЛИС, то в силу ассоциативности операции свертки, результирующая функция отклика получается как свертка функций отклика отдельных систем. Отсюда следует неожиданный вывод о коммутативности последовательного соединения. При параллельном соединении в качестве функции отклика получаем сумму функций, отвечающих отдельным слагаемым.
Вообще говоря, сумма в (1) бесконечная. Чтобы она имела смысл, надо ввести дополнительные ограничения.
Определение.Система (1) называется устойчивой, если она переводит любую ограниченную последовательность в ограниченную.
Предложение. Система устойчива тогда и т.т., когда
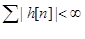 .
.
Доказательство. Достаточность условия очевидна. Для доказательства необходимости заметим, что функция отклика ограничена, поскольку это реакция на ограниченную последовательность. Возьмем в качестве входной последовательности 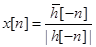 , если
, если 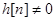 . Реакция в нуле на эту последовательность имеет вид
. Реакция в нуле на эту последовательность имеет вид 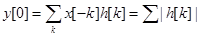 .
.
Дата добавления: 2015-05-13; просмотров: 1826;
