Моделирование технических систем на основе алгебры логики.

Моделирование процессов и объектов машиностроения предполагает, наряду с численными методами, широкое использование математических операций с высказываниями, которые имеют свою специфику и свои законы, рассматриваемые алгеброй логики. Модели алгебры и исчисления высказываний рассматривают связи между высказываниями, которые воспринимаются через выражающие их предложения соответствующего предметного языка.

Овладению им способствует усвоение понятий о простых и составных высказываниях, элементарной алгебры логики. Для спешного решения задач, возникающих при этом, необходимо знание порядка моделирования логических высказываний и технических систем на основе синтеза комбинационных схем. Выражение значительной части знаний, относящихся как к математике, так и к естественному разговорному языку, возможно на основе логической системы – исчисления предикатов первого порядка.

В соответствии с теоретико-множественным подходом в алгебре высказываний в качестве элементов множества выступают простые высказывания, операции над которыми и являются содержанием этой алгебры.

Простое высказывание – каждое утверждение, которое в определенных условиях времени и места может быть истинным или ложным.

Высказывания рассматриваются по отношению к элементам некоторого универсального множества 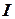. Отдельные элементы этого множества будут обладать различными свойствами и в соответствии с этим могут образовывать различные группы, представляющие собой подмножества множества 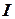. Так, если 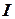– множество инструмента, то его подмножествами могут быть: 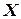– множество резцов; 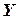– множество сверл; 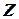– множество зенкеров и т.д.

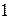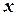Высказывания будем обозначать строчными латинскими буквами и приписывать каждому из них численные значения: (если высказывание истинно) и (если оно ложно). Пусть означает высказывание «это резец». Его численные значения будут равны:

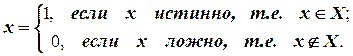
Логической операцией над простыми высказываниями называется построение из них нового составного высказывания. Совокупность таких логических операций получила название алгебры высказываний, или булевой алгебры.

Приняты три способа изображения булевых функций:

1. Формула, указывающая в явном виде последовательность логических операций, производимых над высказываниями 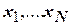,и имеющая вид соотношения.

2. Таблица, указывающая значения истинности составного высказывания в зависимости от значений истинности исходных высказываний. В левой части таблицы перечисляются все возможные комбинации значений истинности исходных высказываний 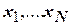, а в правой части – значения истинности составного высказывания . Если имеется N исходных высказываний, то число строк таблицы будет равно .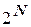

3. Логическая схема, представляющая собой условное графическое обозначение логической операции.

В вычислительной технике и автоматике отдельные высказывания обычно представляются в виде сигналов, имеющих два уровня (0 и 1), или в виде устройств, которые могут принимать два состояния (реле, триггер, транзистор и др). Состояние сигналов в ЭВМ или приборов в системах автоматики определяют значения истинности соответствующих высказываний.

При таком подходе логическая схема представляет собой преобразователь сигналов, который можно использовать для целей управления различными процессами.

Логические операции можно интерпретировать с помощью диаграмм Эйлера – Венна, напоминающих диаграммы геометрической интерпретации тождеств алгебры множеств.