Основы кибернетического моделирования.
В современном научном знании весьма широко распространена тенденция построения кибернетических моделей объектов самых различных классов. «Кибернетический этап в исследовании сложных систем ознаменован существенным преобразованием «языка науки», характеризуется возможностью выражения основных особенностей этих систем в терминах теории информации и управления. Это сделало доступным их математический анализ. Кибернетическое моделирование используется и как общее эвристическое средство, и как искусственный организм, и как система-заменитель, и в функции демонстрационной. Использование кибернетической теории связи и управления для построения моделей в соответствующих областях основывается на максимальной общности ее законов и принципов: для объектов живой природы, социальных систем и технических систем. Широкое использование кибернетического моделирования позволяет рассматривать этот «логико-методологический» феномен как неотъемлемый элемент «интеллектуального климата» современной науки». В этой связи говорят об особом «кибернетическом стиле мышления», о «кибернетизации» научного знания. С кибернетическим моделированием связываются возможные направления роста процессов теоретизации различных наук, повышение уровня теоретических исследований. Рассмотрим некоторые примеры, характеризующие включение кибернетических идей в другие понятийные системы. Анализ биологических систем с помощью кибернетического моделирования обычно связывают с необходимостью объяснения некоторых механизмов их функционирования (убедимся в этом ниже, рассматривая моделирование психической деятельности человека). В этом случае система кибернетических понятий и принципов оказывается источником гипотез относительно любых самоуправляемых систем, т.к. идеи связей и управления верны для этой области применения идей, новые классы факторов. Характеризуя процесс кибернетического моделирования, обращают внимание на следующие обстоятельства. Модель, будучи аналогом исследуемого явления, никогда не может достигнуть степени сложности последнего. При построении модели прибегают к известным упрощениям, цель которых – стремление отобразить не весь объект, а с максимальной полнотой охарактеризовать некоторый его «срез». Задача заключается в том, чтобы путем введения ряда упрощающих допущений выделить важные для исследования свойства. Создавая кибернетические модели, выделяют информационно-управленческие свойства. Все иные стороны этого объекта остаются вне рассмотрения. На чрезвычайную важность поисков путей исследования сложных систем методом наложения определенных упрощающих предположений указывает Р. Эшби. «В прошлом, – отмечает он, наблюдалось некоторое пренебрежение к упрощениям... Однако мы, занимающиеся исследованием сложных систем, не можем себе позволить такого пренебрежения. Исследователи сложных систем должны заниматься упрощенными формами, ибо всеобъемлющие исследования бывают зачастую совершенно невозможны». Анализируя процесс приложения кибернетического моделирования в различных областях знания, можно заметить расширение сферы применения кибернетических моделей: использование в науках о мозге, в социологии, в искусстве, в ряде технических наук. В частности, в современной измерительной технике нашли приложение информационные модели. Возникшая на их основе информационная теория измерения и измерительных устройств – это новый подраздел современной прикладной метрологии. В задачах самых различных классов используется принцип обратной связи.
Кибернетическое моделирование характеризуется тем, что в нём отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «чёрный ящик», имеющий ряд входов и выходов, и моделируют некоторые связи между ними. Чаще всего при использовании кибернетических моделей проводят анализ поведенческой стороны объекта при различных воздействиях внешней среды. Таким образом, в основе кибернетических моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения имитационной модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести на имитационной модели данную функцию, причём на базе совершенно иных математических соотношений и, естественно, иной физической реализации процесса.
Основные понятия корреляционного, регрессионного и дисперсионного анализов
При проведении экспериментов по исследованию различных технических систем (процессов и устройств) и обработке их результатов часто применяют статистические методы, в которых используют стохастические или корреляционные взаимосвязи между параметрами и факторами. Получить, например, математическую модель какого-либо процесса – значит найти математическое описание этих взаимосвязей.
Обычно в задачу корреляционного, регрессионного и дисперсионного анализов входит получение на основании экспериментальных данных математической модели процесса и ее исследование. Методы корреляционного и регрессионного анализа применимы только для таких параметров, которые при изучении физической природы объекта являются взаимосвязанными.
На первом этапе обычно оценивают степень тесноты взаимосвязи значений функции отклика с одной или несколькими независимыми переменными. В первом случае используется коэффициент парной корреляции 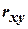 , во втором – коэффициент множественной корреляции
, во втором – коэффициент множественной корреляции 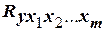 .
.
Коэффициент парной корреляции
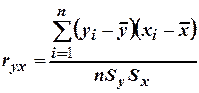 ,
,
где 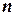 – объем выборки;
– объем выборки; 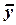 и
и 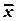 – средние арифметические значения
– средние арифметические значения 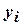 и
и 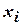 в рассматриваемой выборке;
в рассматриваемой выборке; 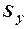 ,
, 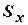 – их средние квадратические отклонения.
– их средние квадратические отклонения.
Коэффициент множественной корреляции с использованием метода определителей находится по формуле
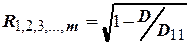 ,
,
где 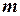 – число независимых переменных;
– число независимых переменных; 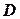 – определитель, составленный из всех коэффициентов парной корреляции;
– определитель, составленный из всех коэффициентов парной корреляции; 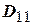 – определитель, получающийся из
– определитель, получающийся из 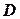 исключением левого столбца и верхней строки.
исключением левого столбца и верхней строки.
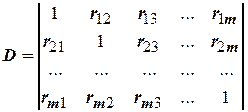 ;
; 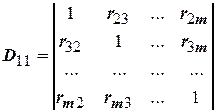
Значения 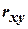 и
и 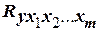 находятся в пределах от -1 до +1. Если они достоверны, т.е. существенно отличаются от 0, значит между исследуемыми факторами имеется линейная корреляционная зависимость. В противном случае эта зависимость отсутствует либо является существенно нелинейной. В результате корреляционным анализом подтверждается наличие взаимосвязей между исследуемыми факторами.
находятся в пределах от -1 до +1. Если они достоверны, т.е. существенно отличаются от 0, значит между исследуемыми факторами имеется линейная корреляционная зависимость. В противном случае эта зависимость отсутствует либо является существенно нелинейной. В результате корреляционным анализом подтверждается наличие взаимосвязей между исследуемыми факторами.
На следующем этапе обработки экспериментальных данных с помощью регрессионного анализа выбирают модель, в наилучшей степени описывающую указанные взаимосвязи. Уравнение, по которому могут быть найдены числовые значения выборочных средних функций отклика при соответствующих значениях независимых переменных, называется уравнением регрессии. В общем случае оно может быть записано в виде
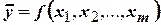 .
.
Одним из универсальных способов получения регрессионных моделей при сглаживании экспериментальных данных является метод наименьших квадратов. За критерий оптимальности модели при этом принимается минимум суммы квадратов отклонений экспериментальных значений функции от предсказанных по уравнению регрессии:
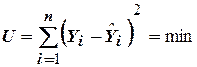 ,
,
где 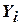 – экспериментальное значение функции при
– экспериментальное значение функции при 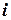 -м значении аргумента;
-м значении аргумента; 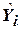 – значение функции, предсказанное уравнением регрессии при том же значении аргумента.
– значение функции, предсказанное уравнением регрессии при том же значении аргумента.
Нетрудно видеть, что выражение под знаком суммы представляет собой площадь квадрата со стороной 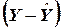 .
.
При построении регрессии в виде прямой линии выражение принимает вид:
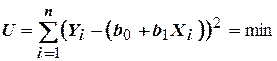 .
.
Здесь 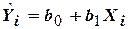 –
– 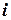 -е значение функции
-е значение функции 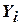 , предсказанное уравнением регрессии первого порядка;
, предсказанное уравнением регрессии первого порядка; 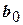 ,
, 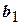 – коэффициенты регрессии.
– коэффициенты регрессии.
Коэффициенты регрессии находятся путем решения системы линейных уравнений:
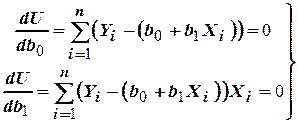 .
.
Ее решение дает возможность рассчитать 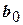 и
и 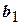 по экспериментальным данным:
по экспериментальным данным:
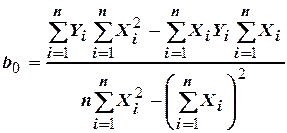 .
.
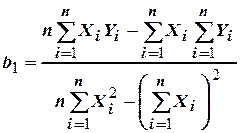 .
.
В технике часто требуется построить модель в виде 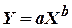 . Для этого ее путем логарифмирования приводят к виду
. Для этого ее путем логарифмирования приводят к виду
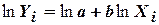 .
.
Для получения искомых величин 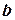 и
и 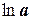 в формулы и вместо истинных значений
в формулы и вместо истинных значений 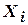 и
и 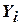 подставляют их логарифмы. В ГОСТ 27.202-83 приводится ряд формул для определения коэффициентов других распространенных зависимостей.
подставляют их логарифмы. В ГОСТ 27.202-83 приводится ряд формул для определения коэффициентов других распространенных зависимостей.
При аппроксимации неизвестных функций отклика в математической статистике часто используют полиномиальные модели, а наиболее часто – простейшие из них – квадратичные.
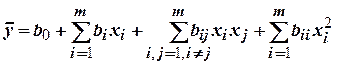
где 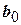 ,
, 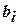 ,
, 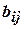 ,
, 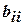 – коэффициенты регрессии.
– коэффициенты регрессии.
С позиций статистики полиномиальная модель удобна тем, что позволяет увеличить степень точности аппроксимации путем повышения порядка полинома.
При определении параметров уравнения регрессии все переменные и соотношения между ними выгодно выражать в стандартизированном масштабе. Значения переменных в стандартизированном масштабе определяются по формуле
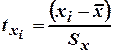 ,
,
где 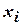 – значения переменных в натуральном масштабе;
– значения переменных в натуральном масштабе; 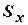 – их среднеквадратичные отклонения от среднеарифметического значения
– их среднеквадратичные отклонения от среднеарифметического значения 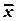 .
.
Статистическое уравнение адекватно описывает результаты опытов, если квадратическое отклонение от экспериментальных данных 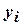 значений зависимой переменной
значений зависимой переменной 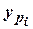 , рассчитанной по уравнению регрессии, обусловлено только ошибкой воспроизведения (т.е. случайным характером этого параметра).
, рассчитанной по уравнению регрессии, обусловлено только ошибкой воспроизведения (т.е. случайным характером этого параметра).
Применение корреляционного и регрессионного анализа правомерно и эффективно при соблюдении ряда условий:
1. Параметр оптимизации 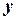 – случайная величина с нормальным законом распределения.
– случайная величина с нормальным законом распределения.
2. Дисперсия 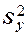 не зависит от абсолютных значений величины
не зависит от абсолютных значений величины 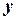 и остается постоянной и однородной при различных наблюдениях
и остается постоянной и однородной при различных наблюдениях 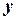 .
.
3. Значения независимых переменных 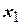 ,
, 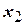 ,…,
,…, 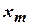 изменяются с пренебрежимо малыми ошибками по сравнению с ошибкой в определении
изменяются с пренебрежимо малыми ошибками по сравнению с ошибкой в определении 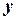 .
.
4. Переменные 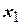 ,
, 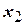 ,…,
,…, 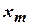 линейно независимы.
линейно независимы.
5. Процесс изменения зависимой переменной 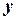 является стационарным и случайным.
является стационарным и случайным.
6. Экспериментальные данные получены из ряда независимых испытаний и образуют случайную выборку из данной генеральной совокупности.
Рассмотрим проверку выполнения этих условий.
1. Соответствие 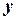 нормальному закону распределения устанавливается либо по большим выборкам с помощью критериев Пирсона или Колмогорова, либо на основании анализа природы величины
нормальному закону распределения устанавливается либо по большим выборкам с помощью критериев Пирсона или Колмогорова, либо на основании анализа природы величины 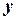 .
.
2. Для оценки однородности дисперсии 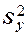 проводят параллельные опыты в различных точках матрицы плана.
проводят параллельные опыты в различных точках матрицы плана.
Однородность ряда дисперсий при одинаковом числе опытов (для определения каждой из них) оценивают с помощью критерия Кохрена – отношения максимальной дисперсии к сумме всех дисперсий ряда.
3. Воспроизводимость опытов и однородность дисперсий достигается, когда выявлены и устранены источники нестабильности эксперимента, а также с помощью более точных средств и методов измерений.
Достаточную точность измерения значений независимых переменных можно проверить, сопоставив ее с диапазоном изменения последних. Считается, что ошибки определения независимых переменных не должны превышать 5…7% интервала их варьирования. Ошибки в определении значений зависимой переменной не влияют столь значительно на точность регрессионного анализа и могут составить до 30% интервала варьирования.
4. Отсутствие коррелированности независимых переменных проверяется расчетом парных коэффициентов корреляции между ними.
5. Случайные процессы называют стационарными в том случае, когда основные характеристики процесса (математическое ожидание, дисперсия и др.) постоянны или однородны во времени. Поскольку при пассивном эксперименте свойства процесса определяются по одной представительной выборке, распространять полученные результаты на весь процесс можно лишь при условии его стационарности.
Поскольку результаты корреляционно-регрессионного анализа, полученные на базе ограниченного числа экспериментальных данных, являются случайными величинами, необходимо оценить их достоверность, определить доверительные интервалы, в которых находятся их истинные значения.
Для этого производится комплекс операций.
1. Оценка достоверности коэффициентов корреляции.
2. Оценка значимости коэффициентов регрессии.
3. Оценка адекватности уравнения регрессии.
Пассивный и активный эксперимент, их место и роль в машиностроении. Основные принципы планирования эксперимента.
Приступая к построению статистической модели, экспериментатор обычно имеет начальные представления о том, как влияют изучаемые факторы на выходные параметры.
При выборе вида модели обычно отвечают на вопрос, допустимо ли представлять функцию отклика линейной или заведомо известно, что зависимости являются немонотонными или сильно нелинейными. В области, где функция отклика имеет экстремум, предположение о линейном характере модели скорее всего не будет подтверждено. Если в дальнейшем потребуется, могут быть проведены дополнительные опыты по уточнению вида модели. При этом результаты первой серии опытов не пропадают и используются в полной мере для построения нелинейной модели.
При планировании экспериментов исходный этап включает определение основного уровня факторов ( 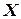 =0) и выбор интервалов варьирования
=0) и выбор интервалов варьирования 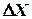 с учетом области действия разрабатываемой модели, предполагаемого характера поверхности отклика и вероятной погрешности определения параметров
с учетом области действия разрабатываемой модели, предполагаемого характера поверхности отклика и вероятной погрешности определения параметров 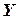 , а также точности фиксирования принятых уровней факторов. Чем больше погрешность опытов и ниже точность поддержания факторов, тем шире должны быть приняты их интервалы варьирования.
, а также точности фиксирования принятых уровней факторов. Чем больше погрешность опытов и ниже точность поддержания факторов, тем шире должны быть приняты их интервалы варьирования.
Рассмотрим основные виды линейных и нелинейных статических моделей 1. При разработке линейной модели ограничиваются обычно варьированием факторов на двух уровнях. Для проведения полного факторного эксперимента (ПФЭ) при 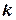 факторах необходимо осуществить
факторах необходимо осуществить 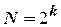 – опытов со всевозможными сочетаниями двух (
– опытов со всевозможными сочетаниями двух ( 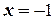 и
и 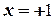 ) уровней факторов (табл.).
) уровней факторов (табл.).
Матрица планирования ПФЭ 23 получается повторением матрицы ПФЭ 22 для факторов 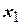 и
и 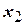 при
при 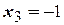 и
и 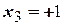 (табл. ).
(табл. ).
| Матрица планирования ПФЭ 22 | ||||
| № опыта | Факторы 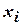
| |||
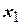
| 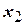
| |||
| + | + | |||
| + | – | |||
| – | + | |||
| – | – | |||
| Матрица планирования ПФЭ 23 | ||||
| № опыта | Факторы 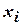
| |||
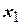
| 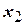
| 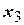
| ||
| + | + | + | ||
| + | – | + | ||
| – | + | + | ||
| – | – | + | ||
| + | + | – | ||
| + | – | – | ||
| – | + | – | ||
| – | – | – | ||
Аналогичным образом могут быть построены матрицы планирования с большим числом факторов, однако при этом число опытов быстро растет и при 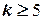 становится весьма значительным. При этом количество опытов (
становится весьма значительным. При этом количество опытов ( 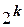 ) намного превышает число неизвестных коэффициентов регрессии (
) намного превышает число неизвестных коэффициентов регрессии ( 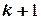 ) линейной модели.
) линейной модели.
Для построения модели с тремя факторами необходимо определить четыре коэффициента (b0, b1, b2, b3), поэтому достаточно всего четырех опытов и можно воспользоваться дробным факторным экспериментом (ДФЭ) –- половиной ПФЭ 23, называемой полурепликой 23-1 . Для этого надо выбрать из опытов матрицы ПФЭ 23 (табл.) такие, в которых бы факторы 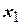 ,
, 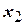 ,
, 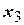 равномерно принимали все возможные значения. Если
равномерно принимали все возможные значения. Если
Матрица планирования
ДФЭ 23-1 ( 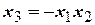 ) )
| |||
| № опыта | Факторы 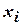
| ||
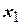
| 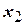
| 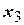
| |
| + | + | – | |
| + | – | + | |
| – | + | + | |
| – | – | – |
воспользоваться генерирующим соотношением, 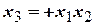 (или
(или 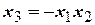 ), то можно получить две антисимметричные экономные матрицы ДФЭ, одинаково пригодные для построения модели
), то можно получить две антисимметричные экономные матрицы ДФЭ, одинаково пригодные для построения модели 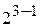 (табл.).
(табл.).
Аналогичным образом могут быть построены полуреплики, четверть реплики и реплики более высокой дробности ПФЭ 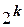 , что дает существенную экономию количества опытов.
, что дает существенную экономию количества опытов.
Так, для 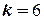 ПФЭ требует проведения
ПФЭ требует проведения 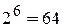 опытов. Однако для определения семи коэффициентов линейного уравнения регрессии задачу можно решать, проведя всего 8 опытов, воспользовавшись ДФЭ
опытов. Однако для определения семи коэффициентов линейного уравнения регрессии задачу можно решать, проведя всего 8 опытов, воспользовавшись ДФЭ 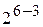 , в котором реплика дробности 1/8. Рекомендуемыми генерирующими соотношениями при этом могут быть
, в котором реплика дробности 1/8. Рекомендуемыми генерирующими соотношениями при этом могут быть 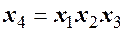 ,
, 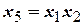 ,
, 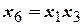 или др.
или др.
Матрица планирования
ДФЭ 24-1 ( 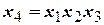 ) )
| ||||||||
| № опыта | Факторы 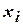
| Взаимодейству-ющие факторы 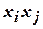
| ||||||
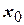
| 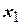
| 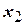
| 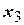
| 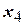
| 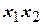
| 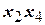
| 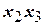
| |
| + | + | + | + | + | + | + | + | |
| + | – | + | + | – | – | – | + | |
| + | + | – | + | – | – | + | – | |
| + | – | – | + | + | + | – | – | |
| + | + | + | – | – | + | – | – | |
| + | – | + | – | + | – | + | – | |
| + | + | – | – | + | – | – | + | |
| + | – | – | – | – | + | + | + | |
| + | ||||||||
| + | ||||||||
| + |
При построении нелинейной модели, учитывающей, кроме линейных членов, также некоторые взаимодействия ( 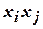 ), в матрицу вводят дополнительные столбцы, содержащие соответствующие произведения факторов (табл.), и увеличивают число опытов.
), в матрицу вводят дополнительные столбцы, содержащие соответствующие произведения факторов (табл.), и увеличивают число опытов.
Так, планируя выявить эффекты взаимодействия факторов 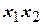 ,
, 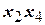 , и
, и 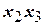 , при
, при 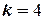 можно воспользоваться восемью опытами, если для построения матрицы экспериментов воспользоваться генерирующим соотношением, например
можно воспользоваться восемью опытами, если для построения матрицы экспериментов воспользоваться генерирующим соотношением, например 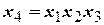 (табл. 3.4). Это позволяет найти четыре коэффициента для линейных членов (b1, b2, b3, b4,), свободный член (b0) и три эффекта взаимодействия (b12, b24, b23).
(табл. 3.4). Это позволяет найти четыре коэффициента для линейных членов (b1, b2, b3, b4,), свободный член (b0) и три эффекта взаимодействия (b12, b24, b23).
Условия проведения опытов задают значения факторов в столбцах 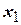 ,
, 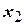 ,
, 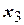 ,
, 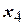 . Столбец
. Столбец 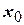 заполнен знаками «+», а столбцы
заполнен знаками «+», а столбцы 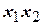 ,
, 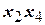 ,
, 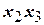 образованы как произведения соответствующих столбцов и применяются при последующем вычислении коэффициентов регрессии.
образованы как произведения соответствующих столбцов и применяются при последующем вычислении коэффициентов регрессии.
Матрицы планирования экспериментов формируются таким образом, чтобы выполнить обеспечивающие простоту вычисления и оптимальные оценки коэффициентов модели требования:
1. Нормировки – сумма квадратов элементов каждого столбца равна числу элементов 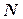
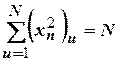 .
.
2. Симметрии – сумма элементов каждого столбца равна нулю
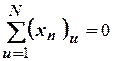 .
.
3. Ортогональности – сумма произведений элементов каждой пары столбцов равна нулю
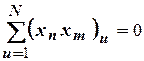 ;
; 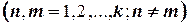 .
.
При выполнении этих требований все коэффициенты регрессии определяются независимо друг от друга с одинаковой погрешностью по результатам всех 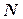 опытов.
опытов.
Ортогональное планирование второго порядка. Рототабельное планирование эксперимента
5.1.1. Ортогональное планирование второго порядка
Если поверхность отклика является существенно нелинейной, тогда в уравнение модели необходимо ввести квадратичные члены второго порядка. Для этого достраивают матрицу в соответствии с планами эксперимента второго порядка .
Расширенная матрица содержит:
- 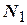 опытов в точках ДФЭ – ядро плана, из которого определяются линейные члены и их взаимодействия;
опытов в точках ДФЭ – ядро плана, из которого определяются линейные члены и их взаимодействия;
- 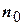 опытов в центре плана, для оценки ошибки опытов;
опытов в центре плана, для оценки ошибки опытов;
- 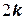 дополнительных опытов в «звездных» точках, расположенных по координатным осям на расстоянии
дополнительных опытов в «звездных» точках, расположенных по координатным осям на расстоянии 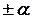 .
.
Отсюда общее число опытов
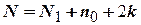 .
.
Число уровней варьирования каждого фактора (-a;-1;0;+1;+a) – 5. Для облегчения вычислений и для того, чтобы параметры модели определялись независимо, план должен быть ортогональным. Это достигается введением вместо 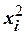 нового нормализованного фактора.
нового нормализованного фактора.
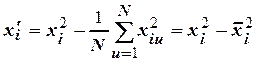 ,
,
где 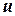 – номер опыта;
– номер опыта; 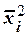 – среднее значение
– среднее значение 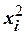 .
.
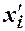 при числе факторов
при числе факторов 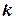 =2,3,4,5 соответственно равняется 0,667;0,73;0,80;0,776 (при
=2,3,4,5 соответственно равняется 0,667;0,73;0,80;0,776 (при 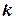 =5 применяется полуреплика). Кроме того, выбирается «звездное» плечо
=5 применяется полуреплика). Кроме того, выбирается «звездное» плечо 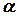 по формуле
по формуле
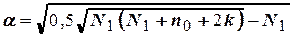 .
.
При ортогональности планирования все параметры нормализованной модели второго порядка определяются независимо друг от друга.
Недостатком центрального композиционного ортогонального планирования (ЦКОП) второго порядка является то, что параметры модели определяются с различной точностью, так как у них различны дисперсии. Поэтому информация о поверхности отклика, содержащаяся в модели, полученной после реализации ЦКОП второго порядка, различна в разных направлениях факторного пространства.
5.1.2. Рототабельное планирование экспериментов
Существует другой способ центрального композиционного планирования второго порядка, позволяющий при помощи полученной модели описывать поверхность отклика с одинаковой точностью по всем направлениям, при этом остаточные дисперсии на одинаковых расстояниях от центра плана являются равными и наименьшими из возможных. Такое планирование получило название рототабельного. При центральном композиционном рототабельном планировании (ЦКРП) значение звездного плеча определяется по формуле
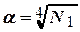 ,
,
где 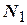 – число опытов ядра плана.
– число опытов ядра плана.
В зависимости от выбора числа опытов в центре плана обеспечивается либо так называемая униформность, либо ортогональность плана. В первом случае дисперсия предсказания сравнительно мало изменяется или совсем не изменяется в радиусе 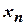 =±1 от центра плана. Для обеспечения униформности плана должно соблюдаться равенство
=±1 от центра плана. Для обеспечения униформности плана должно соблюдаться равенство
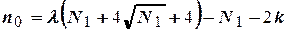 ,
,
в котором 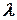 для числа факторов
для числа факторов 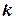 =2,3,4,5,6,7 равно соответственно 0,7844; 0,8385; 0,8705; 0,8918; 0,9070; 0,9185.
=2,3,4,5,6,7 равно соответственно 0,7844; 0,8385; 0,8705; 0,8918; 0,9070; 0,9185.
Чтобы рототабельный план был ортогональным, число опытов в центре плана должно соответствовать равенству
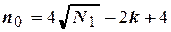 ,
,
полученному из предыдущего при 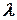 =1. Расчет по нему в некоторых случаях дают дробные значения
=1. Расчет по нему в некоторых случаях дают дробные значения 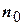 , поэтому их приходится округлять до ближайшего целого числа, нарушая при этом условия униформности. Однако эти отклонения оказываются настолько незначительными, что ими можно пренебречь.
, поэтому их приходится округлять до ближайшего целого числа, нарушая при этом условия униформности. Однако эти отклонения оказываются настолько незначительными, что ими можно пренебречь.
Для построения матриц центрального композиционного рототабельного униформ-планирования (ЦКРУП) рассчитывается и используется ряд характеристик.
Матрицы рототабельного униформ-планирования не ортогональны, поэтому параметры модели рассчитываются более сложным способом, чем при ортогональном планировании.
Так как при планировании экспериментов несколько опытов проводятся параллельно при основном уровне факторов, то их результаты позволяют оценить дисперсию воспроизводимости.
Адекватность модели проверяется при помощи критерия Фишера.
При использовании рототабельных планов исключать из модели без пересчета остальных можно только незначимые оценки 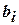 и
и 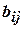 . Исключение любого из незначимых параметров
. Исключение любого из незначимых параметров 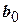 и
и 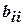 требует пересчета остальных в данной группе.
требует пересчета остальных в данной группе.
При реализации намеченных планированием экспериментов важно учитывать требования рандомизации опытов, т.е. проведения опытов в однородных условиях, с одинаковой погрешностью в случайном порядке. Рандомизация проводится для того, чтобы изменения свойств материалов, характеристик оборудования, средств оснащения, установок и измерительных приборов вследствие их износа и разрушения, смены персонала и т.д. не вызывали искажающего влияния изучаемых факторов и временного «дрейфа» параметров. Поэтому рандомизируют опыты, проводя их в случайном порядке, в отличие от нумерации в матрице планирования.
Дата добавления: 2015-04-03; просмотров: 3447;
