Анализ результатов и принятие решений.

При реализации намеченных планированием экспериментов важно учитывать требования рандомизации опытов, то есть проведения опытов в однородных условиях, с одинаковой погрешностью, в случайном порядке. Рандомизация проводится для того, чтобы изменения свойств материалов, характеристик оборудования, средств оснащения, установок и измерительных приборов вследствие их износа и разрушения, смены персонала и т. д. не вызывали искажающего влияния изучаемых факторов и временного «дрейфа» параметров. Поэтому опыты рандомизируют, проводя их в случайном порядке, отличающимся от нумерации в матрице планирования.

Для оценки дисперсии воспроизводимости, характеризующей ошибку эксперимента, можно либо дублировать опыты матрицы планирования, либо провести серию из n экспериментов в центре плана.

Математические ожидания b_i параметров b_I моделей в соответствии с теорией многофакторного корреляционно-регрессионного анализа находят путём решения системы линейных уравнений, которая в матричной форме имеет вид

X B =Y.

Здесь X, B, Y – соответственно матрицы условий эксперимента, неизвестных коэффициентов b_i и результатов опытов или их логарифмов, которые имеют вид

; ; ,

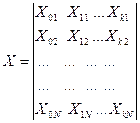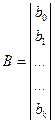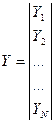где N – число опытов в матрице планирования.

Решение системы линейных уравнений в матричной форме от­носительно коэффициентов b_i имеет вид

.

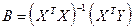Алгоритм обработки экспериментальных данных дан в табл. В ней приняты следующие обозначения: b'_i – кодированное значение i – го коэффициента; X_ij – кодированное значение (+1 или –1) i-го фактора исследуемого процесса в j-м опыте; 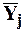– среднее значение выходного параметра процесса в j-м опыте; n – число дублирований каждого опыта; S²{b_i} – дисперсия определения коэффициентов регрессии; S²{Y} – дисперсия опыта; N – число опытов в матрице планирования; 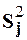{Y}_max– максимальное значение дисперсии среди всех N опытов плана в каждом из которых проводится n повторений.

Коэффициенты 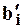справедливы лишь для кодированных значений факторов. По их значениям удобно ранжировать факторы технологического процесса по степени влияния на параметры качества обрабатываемых поверхностей деталей машин, то есть проводить процедуру стратификации.

Значимость влияния того или иного фактора обработки на формирование исследуемого параметра качества детали оценивается по критерию Стьюдента t. Если t_i^расч. ³ t_i^табл., то влияние i-го фактора значимо при выбранном уровне значимости. Полученная модель адекватна, если 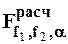£ F^табл. при выбранном уровне значимости a.

Алгоритм построения имитационных моделей

Элементы алгоритма	Расчётная зависимость
Кодирование уровней факторов для моделей	,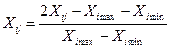
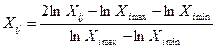
G-критерий Кохрена (расчётное значение)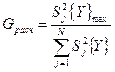
Дисперсия воспроизводимости (дисперсия опыта), если Gрасч£Gтабл)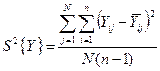
Расчёт кодированных значений коэффициентов регрессий	;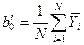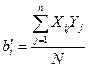
Дисперсия определения коэффициента регрессии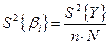
Расчётное значение критерия Стьюдента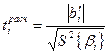
Дисперсия адекватности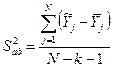
Расчётное значение критерия Фишера	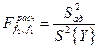, f2 = N – k – 1 и f1 = n – 1 – степени свободы знаменателя и числителя
Значение коэффициентов b0, bi, и их среднее квадратическое отклонение S{bi} для натуральных величин факторов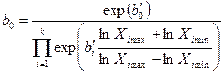

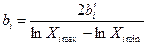
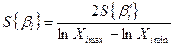
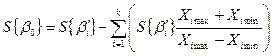
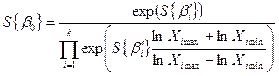
Данная методика статистической обработки результатов технологического эксперимента позволяет получить имитационные модели и определить вероятностные характеристики их параметров b_i, которые имеют нормальное распределение с плотностью

.

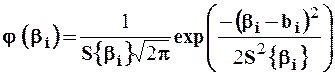Для осуществления необходимых расчётов обычно используется специальное программное обеспечение.