Потоки событий.

Поток событий (ПС) – последовательность однородных событий, появляющихся одно за другим в случайные моменты времени.

Не имеет смысла говорить о вероятности событий, образующих поток, так как в этом случае рано или поздно событие произойдёт и не одно. В этом отличие термина «событие» в понятии поток событий от понятия «случайное событие» в теории вероятностей (это всякий факт, который может произойти или не произойти).

Поток событийявляется в общем случае просто последовательностью случайных точек q₁, q₂, …, q_n на оси времени 0t с разделяющими их случайными интервалами Т₁, Т₂, …, Т_n–1, Т_n, таких, что (рис. 1.1а)

Т₁ = q₂ – q₁; Т₂ = q₃ – q₂; …; Т_n = q_n+1 – q_n.

Простейший ПС обладает тремя свойствами:

1) ординарностью, означающей, что события приходят поодиночке, а не «пачками» по два, три и т. д. ПС ординарный, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мало по сравнению с вероятностью попадания одного события (потоки деталей, поступающих на сборочный конвейер; потоки отказов технических устройств; потоки автомашин, прибывающих на станцию техобслуживания и т. д.);

2) отсутствием последействия, означающим, что события, образующие поток, появляются в последовательные случайные моменты времени независимо друг от друга. ПС без последействия наблюдается, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой;

3) стационарностью – однородностью по времени, то есть постоянством его статистических характеристик. ПС стационарен, если вероятность попадания того или иного числа событий на участке времени t зависит только от длины участка и не зависит от того, где этот участок находится на оси t.

Для ординарного потока событий весьма важно понятие «интенсивность потока» l(t):

l(t) = .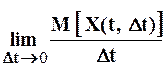

Здесь X(t, Dt) – случайное число событий, попадающих на элементарный участок (t, t+Dt).

Физический смысл интенсивности l(t) потока событий – это среднее число событий, приходящееся на единицу времени, для элементарного участка Dt, примыкающего к t.

Интенсивность ПС может быть любой неотрицательной функцией времени (l(t) ³ 0) и имеет размерность [1/время]. Для стационарного ПС интенсивность постоянна (l(t) = const).

Простейший поток событий называют ещё стационарным пуассоновским потоком, для которого вероятность того, что на участке времени длины t наступит ровно k событий, определяется по зависимости

,

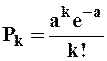где a = lt – среднее число событий, приходящееся на участок t.

Такой поток назван простейшим потому, что исследование систем, находящихся под воздействием простейших потоков, проводится самым простым образом.