Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова - старшего (1856 - 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 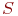 имеет
имеет 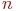 возможных состояний:
возможных состояний: 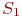 ,
, 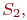 ...,
..., 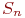 . Вообще говоря, число состояний может быть бесконечным. Однако модель, как правило, строится для конечного числа состояний.
. Вообще говоря, число состояний может быть бесконечным. Однако модель, как правило, строится для конечного числа состояний.
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 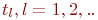 . В дальнейшем будем называть временные точки
. В дальнейшем будем называть временные точки 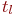 шагами.
шагами.
Известны вероятности перехода  системы за один шаг из состояния
системы за один шаг из состояния  в состояние
в состояние 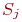 .
.
Цель моделирования: определить вероятности состояний системы после  -го шага.
-го шага.
Обозначим эти вероятности 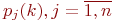 (не путать с вероятностями
(не путать с вероятностями  ).
).
Если в системе отсутствует последействие, то есть вероятности  не зависят от предыстории нахождения системы в состоянии
не зависят от предыстории нахождения системы в состоянии  , а определяются только этим состоянием, то описанная ситуация соответствует модели дискретной марковской цепи.
, а определяются только этим состоянием, то описанная ситуация соответствует модели дискретной марковской цепи.
Марковская цепь называется однородной, если переходные вероятности  от времени не зависят, то есть от шага к шагу не меняются. В противном случае, то есть если переходные вероятности
от времени не зависят, то есть от шага к шагу не меняются. В противном случае, то есть если переходные вероятности 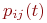 зависят от времени, марковская цепь называется неоднородной.
зависят от времени, марковская цепь называется неоднородной.
Значения  обычно сводятся в матрицу переходных вероятностей:
обычно сводятся в матрицу переходных вероятностей:
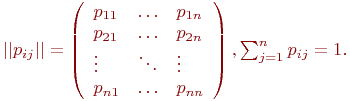
Значения  могут также указываться на графе состояний системы. На рис. показан размеченный граф для четырех состояний системы. Обычно вероятности переходов «в себя» -
могут также указываться на графе состояний системы. На рис. показан размеченный граф для четырех состояний системы. Обычно вероятности переходов «в себя» -  ,
, 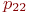 и т. д. на графе состояний можно не проставлять, так как их значения дополняют до 1 сумму переходных вероятностей, указанных на ребрах (стрелках), выходящих из данного состояния.
и т. д. на графе состояний можно не проставлять, так как их значения дополняют до 1 сумму переходных вероятностей, указанных на ребрах (стрелках), выходящих из данного состояния.
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 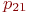 ,
, 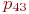 и др.
и др.
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
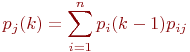
где 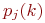 - вероятность
- вероятность 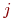 -го состояния системы после
-го состояния системы после  -го шага,
-го шага, 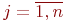 ;
;
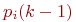 - вероятность
- вероятность 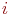 -го состояния системы после
-го состояния системы после  -го шага,
-го шага, 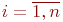 ;
;
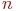 - число состояний системы;
- число состояний системы;
 -переходные вероятности.
-переходные вероятности.
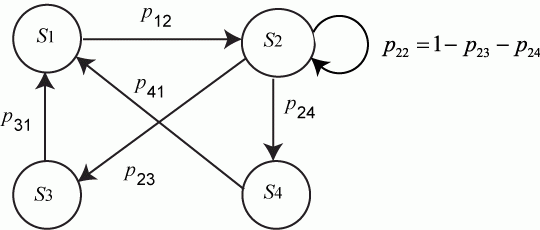
Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
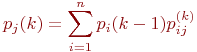
где 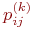 - значения переходных вероятностей для
- значения переходных вероятностей для  -го шага.
-го шага.
Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то - занятость. Если состояния объектов, то - поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 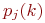 .
.
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 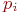 , так как вероятность «перескока» системы из одного состояния в другое точно в момент времени
, так как вероятность «перескока» системы из одного состояния в другое точно в момент времени  равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов  :
:
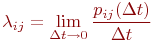
где 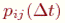 - вероятность того, что система, находившаяся в момент времени
- вероятность того, что система, находившаяся в момент времени  в состоянии
в состоянии  за время
за время 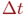 перейдет в состояние
перейдет в состояние 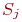 .
.
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
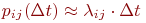
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов  не зависят от времени
не зависят от времени  (от момента начала промежутка
(от момента начала промежутка 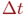 ). В противном случае непрерывный марковский процесс называется неоднородным.
). В противном случае непрерывный марковский процесс называется неоднородным.
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 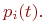 Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов  .
.
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 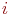 -го состоянии
-го состоянии 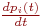
5. В правой части записывается алгебраическая сумма произведений 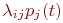 и
и 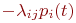 . Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус.
. Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус.
6. Определить начальные условия и решить систему дифференциальных уравнений.
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
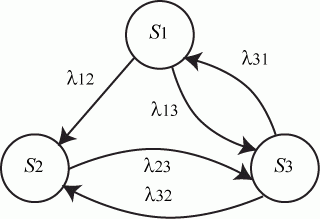
Рис. Размеченный граф состояний
Решение:
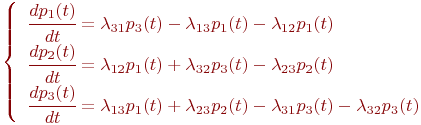
Очевидно, 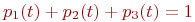 .
.
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 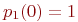 ,
, 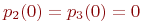 .
.
Дата добавления: 2015-04-03; просмотров: 9837;
