Критерии оптимизации моделей в машиностроении.

Большой и важный класс математических моделей технических систем составляют системы уравнений и неравенств. Оптимальная система управления, например производственным процессом, может быть реализована в виде набора правил, стратегии или способа управления, или в виде комплекса средств управления, согласно которым следует поступать в той или иной ситуации. Методы оптимизации базируются на системном подходе, сущностью которого в этом случае является комплексное, единое рассмотрение всех частей процесса или системы и гармоническое их сочетание. Особенно ценна роль системного подхода в поэтапном решении задачи оптимизации, которая включает в себя при проектировании любой системы почти одни и те же этапы, на каждом из которых встаёт проблема формулировки критериев оптимальности и оптимизации. Однако системный подход подразумевает их общую оптимизацию: в отдельности каждый из этапов может и не быть оптимальным.

Одним из самых важных и в то же время далёких от удовлетворительного решения является вопрос о критериях оптимизации. Достаточно грамотно формулировать критерии управления можно с помощью прагматики – науки, которая занимается определением целей и задач управления, изучением значения и ценности результатов поведения, движения, развития и управления системами. От чисто качественного, неформализованного характера методы прагматики отличаются более высоким уровнем формализации с помощью семиотики и математической лингвистики:

Семиотика (от греч.-знак) – комплекс научных теорий, изучающих свойства знаковых систем, т.е. систем конкретных или абстрактных объектов (их называют знаками), с каждым из которых определённым образом сопоставлено некоторое значение.

· Математическая лингвистика – прикладная математическая дисциплина, основной задачей которой является разработка точных методов исследования естественных языков. В ней широко используются методы теории алгоритмов, теории автоматов и алгебры. Эта наука включает в себя три основных раздела: 1) разработка и изучение способов описания структуры отрезков речи; 2)изучение формального строения лингвистически значимых отношений и классификаций на множествах языковых объектов; 3)теория формальных грамматик. Эти разделы отвечают трём аспектам формального описания языка.

Выбор конкретного критерия оптимизации зависит от конструктора системы или технолога, и в этом содержится элемент нестрогости. На практике всё чаще используют типовые критерии, которые становятся общепринятыми и заносятся в технические задания.

При решении задач оптимизации необходимо различать понятия функции и функционала. В математике понятие функционала является дальнейшим обобщением понятия функции. Не очень строго функционал можно определить как функцию от функции, т.е. функцию, в которой в качестве независимой переменной выступает функция.

Рассмотрим наиболее распространённые виды критериев оптимизации и области их применения:

1. Критерий среднего квадрата ошибки.Применяется при оценке качества работы автоматической системы регулирования (АСР) и при решении математических задач оптимизации.

2. Интегральный критерий.Используется для определения параметров АСР, оптимальной в переходном процессе.

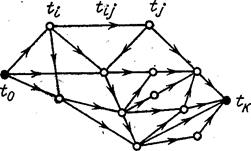
3. Критерий максимального быстродействия.При определении параметров АСР в режиме переходного процесса часто используют критерий оптимальности, обеспечивающий её быстродействие, т.е. переходный процесс должен заканчиваться в минимальное время. Выполнение этого требования повышает качество обработки деталей при использовании копировальных следящих систем. В этом случае следящая система должна отрабатывать входной сигнал с отсутствием (в идеале) колебательности

4. Критерий минимума стоимости.В данном случае рассматривается функционал, определяющий стоимость функциони­рования совокупности систем массового обслуживания (или сети массового обслуживания) в единицу времени:

Случайность потока заявок и времени их обслуживания обуславливают какое-то среднее число простаивающих ячеек обслуживания или ожидающих заявок. Для оптимизации работы системы массового обслуживания необходимо, чтобы 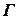=min.

Такую модель и критерий можно использовать в машиностроении в различных ситуациях, например при организации службы по ремонту оборудования. В этом случае ячейку обслуживания представляет ремонтная бригада, а заявку – отказы оборудования. Минимум функционала означает оптимальный выбор числа бригад, основанный на определённой статистике потока отказов оборудования.

а)   в) д)

б)     г)

Рис. Интерпретация критериев оптимизации:

а – к определению ошибки АСР; б – оценка качества работы АСР по величинам дисперсии или модуля ошибки; в – интегральный критерий качества; г – оптимальная по быстродействию система;

д – пример сетевого графика

5. Критерий минимума критического времени выполнения работы.Этот критерий используется при оптимизации сетевых моделей планирования и управления производственным процессом. Примером может служить процесс конструкторско-технологической подготовки производства для выпуска новой продукции и другие ситуации, когда выполнение поставленной задачи сводится к выполнению определённого количества работ и возникает вопрос о критическом пути.

6. Минимаксный критерий.Этот критерий широко используется для определения оптимальной стратегии принятия решений при наличии конфликтной ситуации, что для условий производства означает наличие конкуренции в различных сферах (сбыт, обслуживание и т.д.). В такой ситуации интересы двух сторон противоположны, так как выигрыш одной стороны означает проигрыш другой. Поэтому приходится выбирать среди худших для себя стратегий конкурента (противника) наименее худшую, т.е. брать максимум по множеству стратегий противника и минимум по собственным стратегиям