Алгоритмы. Основы разработки алгоритмов. Блок-схемы алгоритмов
| ky | x, м | l, м | dy ,м | dyср, м | Ddy ,м | e, % |
| 0,005 | 1,2656*10-4 | 1,2657*10-4 | 1,27*10-5 | 10,05 | ||
| -1 | -0,005 | 1,2656*10-4 | 1,27*10-5 | 10,05 | ||
| 0,01 | 1,2657*10-4 | 6,39*10-6 | 5,05 | |||
| -2 | -0,01 | 1,2657*10-4 | 6,39*10-6 | 5,05 | ||
| 0,015 | 1,2657*10-4 | 4,28*10-6 | 3,38 | |||
| -3 | -0,015 | 1,2657*10-4 | 4,28*10-6 | 3,38 |
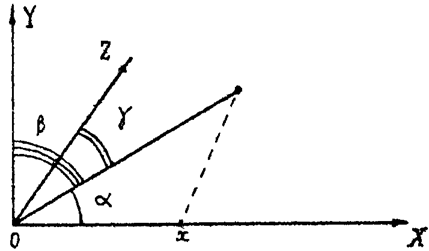
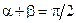 , откуда
, откуда
cos a = sin g;
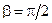 ;
;
z = l;
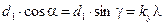 ;
;
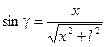 ;
;
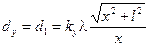 (3.1)
(3.1)
Расчет погрешностей:
Для расчета погрешностей воспользуемся формулой
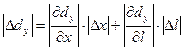 . (3.2)
. (3.2)
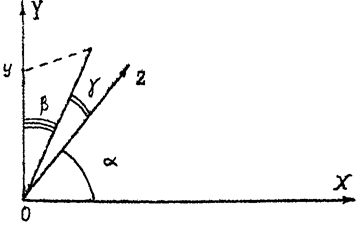
Из формулы (3.1) следует
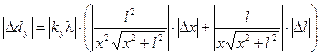 , (3.3)
, (3.3)
где Dx = Dl = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
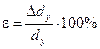 . (3.4)
. (3.4)
| kx | y, м | l, м | dx ,м | dxср, м | Ddx ,м | e, % |
| 0,005 | 1,2656*10-4 | 1,2657*10-4 | 1,27*10-5 | 10,05 | ||
| -1 | -0,005 | 1,2656*10-4 | 1,27*10-5 | 10,05 | ||
| 0,01 | 1,2657*10-4 | 6,39*10-6 | 5,05 | |||
| -2 | -0,01 | 1,2657*10-4 | 6,39*10-6 | 5,05 | ||
| 0,015 | 1,2657*10-4 | 4,28*10-6 | 3,38 | |||
| -3 | -0,015 | 1,2657*10-4 | 4,28*10-6 | 3,38 |
Согласно рассуждениям из первой части опыта, аналогично получаем:
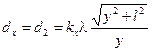 (3.5)
(3.5)
Из формул (3.2) и (3.5) получаем:
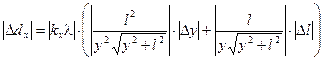 , (3.6)
, (3.6)
где Dy = Dl = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
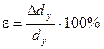 (3.7)
(3.7)
Для третьей части опыта:
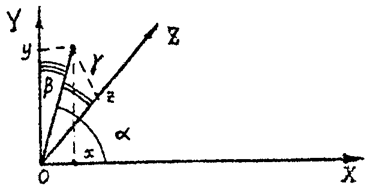
z = l,
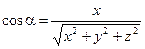 ,
,
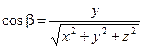 ,
,
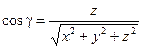 ,
,
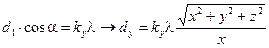 (3.8)
(3.8)
(3.9)
Погрешности вычисляю по формулам:
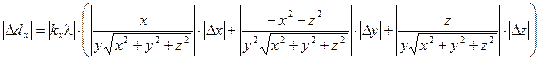 (3.10)
(3.10)
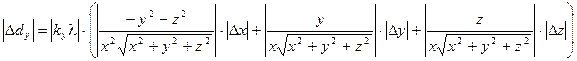 (3.11)
(3.11)
где Dx = Dy = Dz = 0,0005 м.
Относительную погрешность вычисляю по формуле, аналогичной (3.4) и (3.7).
| kx | ky | x, м | y, м | l, м | dx, м | dy, м | dxcp, м | dycp, м | Ddx, м | ex, % | Ddy, м | ey, % |
| 0,005 | 0,01 | 6,33*10-5 | 2,53*10-4 | 1,27*10-4 | 1,83*10-4 | 3,20*10-6 | 5,05 | 2,54*10-5 | 10,05 | |||
| -1 | -0,005 | 0,015 | 4,22*10-5 | 3,80*10-4 | 1,43*10-6 | 3,38 | 3,82*10-5 | 10,05 | ||||
| -3 | 0,01 | -0,015 | 8,44*10-5 | 1,90*10-4 | 2,86*10-6 | 3,38 | 9,59*10-6 | 5,05 | ||||
| -3 | -2 | -0,015 | -0,01 | 1,90*10-4 | 8,44*10-5 | 9,59*10-6 | 5,05 | 2,86*10-6 | 3,38 | |||
| -1 | 0,01 | 0,005 | 2,53*10-4 | 6,33*10-5 | 2,54*10-5 | 10,05 | 3,20*10-6 | 5,05 | ||||
| -3 | 0,015 | -0,015 | 1,27*10-4 | 1,27*10-5 | 4,28*10-6 | 3,38 | 4,28*10-6 | 3,38 |
Вывод: в результате эксперимента были получены параметры двумерной дифракционной решетки (1,27*10-4 м). Погрешность составила не более 10%.
Алгоритмы. Основы разработки алгоритмов. Блок-схемы алгоритмов
Алгоритм - это точное предписание исполнителю совершить последовательность действий, направленных на достижение поставленной цели. Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде псевдокодов, формул, или записанным на каком-либо языке программирования.
Наиболее популярным для решения задач на ЭВМ является графическая форма представления алгоритма в виде блок-схем. Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, что облегчает процесс написания программы, ее корректировки при возможных ошибках.
Алгоритм любой сложности может быть представлен комбинацией трех базовых структур:
· линейная;
· разветвляющая (альтернатива);
· циклическая.
Характерной особенностью этих структур является наличие у них одного входа и одного выхода.
Базовая структура "линейная" (следование) означает, что несколько операторов должны быть выполнены последовательно друг за другом и только один раз за время выполнения данной программы (рис. 1). Под оператором понимается формальная запись команды для выполнения некоторого действия.
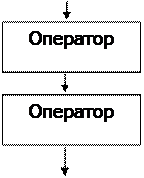 | |||
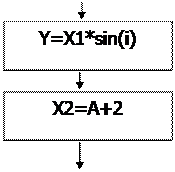 | |||
Рисунок 1- Базовая структура «Линейная»
Базовая структура "разветвляющая" обеспечивает, в зависимости от результата проверки условия (истинна или ложь), выбор одного из альтернативных путей работы алгоритма (рис. 2).
 | 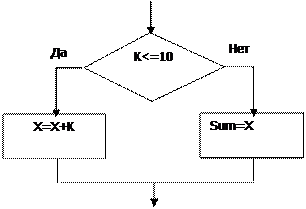 |
Рисунок 2- Базовая структура «Разветвляющая»
Алгоритм, в состав которого входит базовая структура " альтернатива или разветвляющая", называется разветвляющимся.
Третья базовая структура "циклическая" обеспечивает повторное выполнение или, другими словами, циклическую работу операторов.
Различают три разновидности этой структуры:
· "цикл - пока" (рис. 3 а);
· "цикл - до" (рис. 3 в);
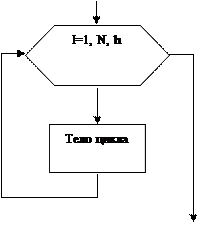
· Цикл с заданным числом повторений (рис. 3 с).
 | |||||
 | |||||
 | |||||
а) в) с)
а) – цикл - пока;
в) – цикл - до;
с) – цикл с заданным числом повторений.
Рисунок 3- Базовая структура «Циклическая»
Группа операторов, повторяющихся в цикле, называются телом цикла. Основное отличие структуры "цикл - пока" от структуры "цикл - до" заключается в том, что в первой структуре операторы тела цикла в зависимости от условия могут не выполняться совсем, тогда как в структуре "цикл - до" тело цикла будет выполняться хотя бы один раз. Можно заметить, что в структуре "цикл - пока" проверка выполнения условия осуществляется перед выполнением операторов тела цикла, а в структуре "цикл - до" - после прохождения тела цикла.
Цикл с заданным числом повторений обозначает повторение некоторых действий указанное число раз.
Циклы могут содержать внутри себя другие циклы. Такие структуры называются вложенными циклами. Алгоритмы, имеющие в своем составе базовую структуру "цикл", называются циклическими.
Реальные алгоритмы представляют собой совокупность всех рассмотренных базовых структур.
Основные свойства алгоритмов: дискретность, определенность, конечность, повторяемость и универсальность (массовость).
Дискретность означает, что выполнение алгоритма разбивается на последовательность законченных действий - шагов.
Определенностьозначает, что каждое правило алгоритма настолько четко и однозначно, что значения величин, получаемые на каком-либо шаге, однозначно определяются значениями величин, полученными на предыдущем шаге, и при этом точно известно какой шаг будет выполнен следующим.
Конечность(результативность) алгоритма предполагает, что его исполнение сводится к выполнению конечного числа шагов и всегда приводит к некоторому результату. Бесконечных алгоритмов не бывает.
Повторяемостьалгоритма предполагает, что при многократных расчетах с одними и теми же исходными данными результат должен повторяться.
Массовость(универсальность) означает, что алгоритм решения задачи разрабатывается в общем виде так, чтобы его можно было применить для множества задач одного класса, различающихся лишь набором исходных данных.
При блок-схемном описании алгоритм изображается различными геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий, проверка выполнения условия, ввод или вывод данных и др. Для каждого действия предусмотрена своя геометрическая фигура. В таблице 1 представлены основные блоки и их назначение.
Таблица 1. Основные блоки
| Наименование | Обозначение | Функции |
| Процесс | 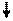  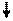
| Выполнение операций, в результате которых изменяется значение, форма представления или расположение данных. |
| Ввод-вывод (данные) | 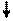  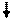
| Ввод данных в программу, или отображение (вывод) результатов работы программы на экране дисплея. |
| Условие (решение) |   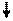 
| Выбор направления выполнения алгоритма в зависимости от некоторых переменных условий. |
| Модификация | 
| Отображает цикл. В блоке указываются начальное значение цикла, его шаг и условие окончания цикла. |
| Предопределённый процесс (подпрограмма) | 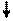 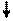 
| Использование ранее созданных и отдельно написанных программ (подпрограмм). |
| Документ |  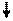
| Вывод данных на бумажный носитель. |
| Пуск (начало) |  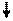
| Начало процесса обработки данных (алгоритма). |
| Стоп (конец) | 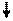 
| Конец (завершение) процесса обработки данных (алгоритма). |
| Соединитель (узел) |    
| Указание связи между прерванными линиями, соединяющими блоки. N – номер связи. |
| <== предыдущая лекция | | | следующая лекция ==> |
| Выполнение опыта | | | Основы системного программного обеспечения. Основные элементы операционных систем (команды, утилиты). |
Дата добавления: 2015-04-01; просмотров: 4193;
