Графовые модели технических объектов и технологических процессов в машиностроении.

Модели в виде графов получили широкое распространение в науке и технике, в частности в машиностроении, благодаря дополнительным возможностям, которые появляются при геометрическом подходе к трактовке и решению различных процессов в сфере проектирования, производства и управления. Это обусловлено тем, что в отличие от евклидовых, прямоугольных, криволинейных и других пространств в графовых моделях используются концепции топологических геометрий и пространств.

Основу прикладной теории графов как научной дисциплины составляет совокупность представлений и методов, сформировавшихся при решении конкретных задач.

Используя простую терминологию, можно сказать, что граф характеризует отношения между множествами объектов и теория графов направлена на исследования некоторых из многих возможных в заданном представлении свойств этих объектов. Более строго, в пространственно-временной области, граф есть совокупность точек и линий, соединяющих эти точки. Эти соединения могут обладать многими характеристиками, и теория графов занимается изучением этих характеристик.

В машиностроении в виде графов широко представляются задачи построения технологических процессов механической обработки деталей, сборки изделий, вопросы исследования механизма технологического наследования и многие другие.

В основе теории графов лежит теория множеств. граф является универсальным средством наглядного представления большого числа теоретических и практических задач. Наглядно граф изображается в виде множества точек 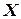плоскости, называемых вершинами, и множестванаправленных отрезков 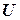, соединяющих все или некоторые из вершин, называемых дугами.

Математически граф 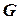можно определить как пару указанных множеств 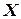и :

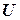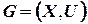
Вершины графа 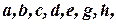а его дугами являются отрезки 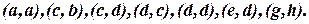Если считать, что множество направленных дуг 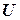, соединяющих элементы множества 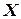, отображает это множество само в себя, то граф можно считать заданным, если дано множество его вершин 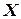и способ отображения 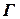множества 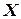в 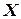, т.е. граф 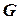есть пара 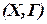, состоящая из множества 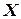и отображения 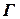, заданного на этом множестве:

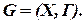
Для графа на рис. отображение 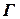определено следующим образом:

; ; ; ; ; .

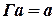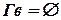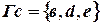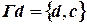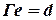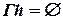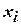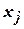
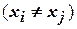Граф называется полным, если для любой его пары вершин и существует дуга .

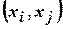Пусть 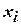есть подмножество вершин графа 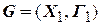. Тогда граф 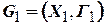, множество вершин которого совпадает с 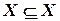, а множество дуг 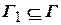включает все дуги множества 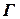с концевыми вершинами только из множества 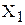, называется подграфом графа 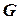, порожденным множеством .

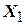Граф называется планарным, если он может быть изображен на плоскости так, чтобы его ребра пересекались только в вершинах.

Плоская карта – это планарный граф вместе с областями, простые циклы которого разделяют плоскость таким образом, что каждое ребро является границей двух областей. (Два ребра, являющихся границами смежных областей, могут быть заменены одним ребром, разделяющим эти две области.). В более общей формулировке карта 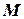– это граф 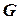вместе с поверхностью 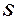, на которой 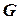нанесен таким образом, что его ребра пересекаются только в их граничных точках. Говорят, что карта 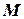является укладкой графа 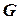на поверхности .

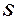Правильной раскраской карты в 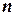цветов ( 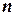-раскраской) называют такую, когда каждая из областей раскрашивается в один из 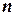цветов и ни одна пара смежных областей не окрашивается одним цветом.

Подграфом 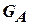графа 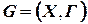называется граф, в который входит лишь часть вершин графа 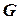, образующих множество 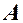, вместе с дугами, соединяющим эти вершины.

;

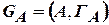
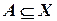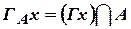
Связные подграфы, на которые может быть разбит несвязный граф, называются его компонентами или частями.

Фактором графа 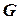называется подграф, который включает все его вершины, но не является вполне несвязным. Регулярный подграф степени 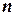является 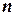-фактором. Граф 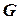является суммой факторов, если он представляет собой объединение непересекающихся множеств их ребер. В этом случае имеют дело с факторизацией графа .

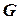Частичным графом 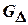по отношению к графу 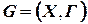называется граф, содержащий только часть дуг графа 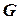, т.е. определяемый условием:

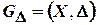, где .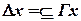

На рис. очерченная пунктиром область является подграфом 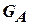: 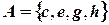; 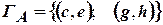, а граф, образованный жирными дугами, является частичным графом

: , .

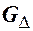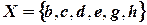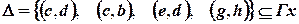Другие важные понятия – путь и контур.

Путь в графе 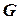– последовательность дуг 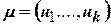, в которой конец каждой предыдущей дуги совпадает с началом следующей. Путь 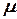, последовательными вершинами которого являются вершины 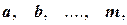обозначается через .

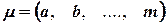Простой путь – путь, в котором никакая дуга не встречается дважды. Это так называемый Эйлеров путь. Эйлер доказал, что в любом конечном связном графе, где все вершины четны (количество дуг, входящих и выходящих из вершины четно) или содержится не более двух вершин нечетной степени, существует путь, в котором каждая дуга участвует ровно один раз.

Если граф содержит точно две вершины нечетной степени, то в Эйлеровом пути эти вершины должны быть конечными. Если вершин нечетной степени нет, то граф имеет замкнутый Эйлеров путь (Эйлеров контур).

Элементарный путь – путь, в котором никакая вершина не встречается дважды (Гамильтоновый путь).

Граф 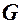называется гамильтоновым, если он содержит простой цикл (называемый гамильтоновым циклом), проходящий через все его вершины. Полный граф всегда содержит гамильтонов цикл.

Простая формулировка часто рассматриваемой задачи о коммивояжере состоит в следующем. Требуется найти путь коммивояжера, которому необходимо последовательно обойти (n-1) пунктов, заходя в каждый пункт только один раз, и вернуться в исходный пункт, причем общая протяженность его пути должна быть минимальна. Таким образом, среди всех гамильтоновых циклов полного графа с 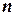вершинами нужно найти такой, общая длина ребер которого минимальна. Задача о коммивояжере эквивалента задаче о последовательности выполнения различных операций на одном агрегате, когда требуется минимизировать общее время переналадки (т.е. время подготовки оборудования к последующей операции). В этом случае каждому пункту соответствует определенный вид операции, расстоянию межу пунктами – время переналадки для каждой операции, а общей протяженности пути – суммарное время переналадки.

Поиск и нахождение эквивалентностей между известными теоретическими решениями в одних областях и возникающими задачами в других, в частности в машиностроении, является одной из главных целей исследователя и искусством, которому следует учиться.

Неориентированным графом называют граф без учета ориентации дуг.

Для неориентированного графа понятия дуга, путь и контур заменяются понятиями ребро, цепь, цикл. Ребро – это отрезок, соединяющий две вершины. Граф на рис. имеет восемь дуг, но семь ребер. Цепью называется последовательность ребер, циклом – конечная цепь, у которой начальная и конечная вершины совпадают.

Граф связен, если любые две его вершины можно соединить цепью. Если граф 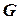не связен, то его можно разбить на такие подграфы 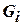, что все вершины в каждом подграфе связны, а вершины из различных подграфов не связны. Такие подграфы 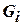называются компонентами связности графа .

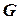Вершина графа, после удаления которой он становится несвязным, называется точкой сочленения. Связность графа – наименьшее число вершин, удаление которых делает граф несвязным.

Разрез графа – минимальное множество ребер, удаление которых увеличивает число компонент.

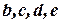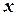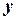
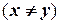Для того чтобы определить связность ориентированного графа, не нужно обращать внимание на ориентацию дуг. Граф, изображенный на рис. не является связным. Однако его подграф, состоящий из вершин , является связным. Ориентированный граф сильно связен, если для любых двух вершин и существует путь, идущий из 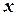в .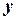

Деревом (важный частный случай неориентированного графа) называется конечный связный неориентированный граф, не имеющий циклов. Для множества вершин 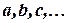дерево строится следующим образом. Одну из вершин, например 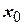,примем за начальную и назовем ее корнем дерева. Из этой вершины проводим ребра в близлежащие вершины 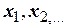из них проводим ребра в соседние с ними вершины 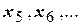и т.д., т.е. дерево можно построить, последовательно добавляя ребра в его вершинах. Это дает возможность установить связь между числом вершин и числом ребер дерева: дерево с 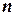вершинами имеет 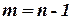ребер. В неориентированном графе дерево представляет собой связный подграф, не имеющий циклов.

Покрывающее дерево – дерево, которому принадлежат все вершины графа. Ориентированное дерево имеет корень в вершине 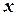, если существует путь от 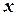к каждой из других вершин. Ребра графа, принадлежащие покрывающему дереву, называются ветвями, все остальные – хордами.

Примеры некоторых графов даны на рисунке. Они и подобные им могут использоваться для интерпретации и решения различных производственных задач.

Для описания свойств графа на множествах его вершин и дуг (ребер) рассматриваются специфические для графов отношения – смежности и инцидентности.

Смежность характеризует отношение между элементами одноименных множеств 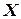и 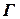. Различные вершины называются смежными, если они соединены дугой (ребром). Различные дуги (ребра) называются смежными, если они имеют общую концевую вершину.

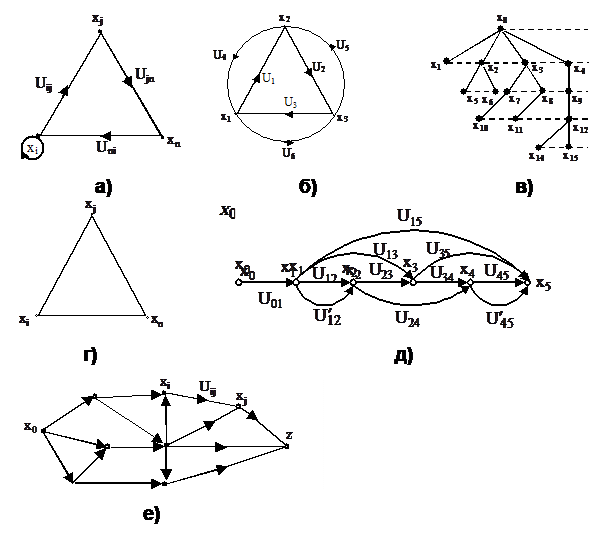Примеры графов:

а – с петлей; б – симметричный; в– в виде дерева; г – неориентированный;

д – ориентированный; е – в виде сети

Инцидентность характеризует отношение между элементами разноименных множеств 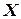и 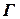. Дуга и вершина инцидентны, если вершина является для дуги концевой вершиной.

Степенью вершины 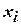( 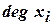или 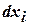) для неориентированного графа называют число ребер, инцидентных вершине .

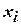Если 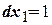– вершина тупиковая, а если 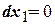– вершина изолированная.

Доказано, что для неориентированного графа с 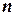вершинами и 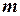ребрами сумма степеней вершин составляет 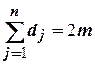– четное число.

Связный граф называется регулярным, если все его вершины имеют одинаковую степень. Кратностью пары вершины называется число соединяющих их ребер. Следовательно, в каждом графе число вершин нечетной степени четно.

Для ориентированных графов свойственны:

полустепень исхода вершины 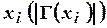– число дуг, исходящих из вершины ;

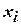полустепень захода вершины 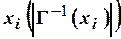– число дуг, заходящих в вершину .

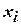Ориентированным графом, не имеющим петель и контуров, удобно представлять технологические процессы обработки деталей и сборки узлов, а также другие в широком смысле операции машиностроительных производств.

Графы удобно представлять в виде некоторых матриц. Особенно часто встречаются описания графов в виде матриц смежности и инциденций.

Обозначим через 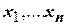вершины графа, а через 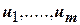его дуги. Введем числа:

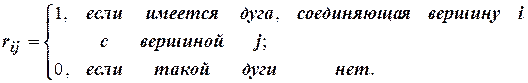
Квадратная матрица 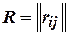порядка 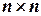, строки и столбцы которой соответствуют вершинам, называется матрицей смежности вершин графа. В случае неориентированного графа элемент матрицы 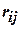равен числу ребер, соединяющих вершины 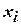и .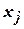

Матрица смежности ребер – матрица, строки и столбцы которой соответствуют ребрам графа, а элемент 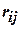равен числу вершин, инцидентных двум ребрам 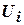и .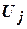

Введем, далее, числа

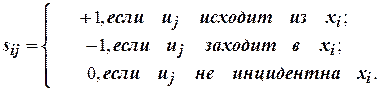
Матрица 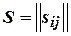порядка 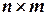, строки которой соответствуют вершинам, а столбцы – ребрам, называется матрицей инциденций для дуг графа.

Для неориентированного графа элемент матрицы инциденций 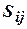равен 1, если вершина инцидентна ребру. В противном случае .

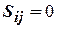Матрицы инциденций в описанном виде применимы только к графам без петель. При наличии в графе петель эту матрицу следует расчленить на две полуматрицы: положительную и отрицательную.

Два графа называются изоморфными тогда и только тогда, когда имеется взаимно-однозначное соответствие между их вершинами и ребрами при сохранении отношений инцидентности.