Средства математического моделирования технических объектов и обеспечение.

Особенностью использования математического моделирования на современном этапе стало применение ЭВМ, что явилось решающим условием широкого внедрения аналитических методов в исследование сложных производственных систем.

Обычно модель строится по иерархическому принципу, когда последовательно анализируются отдельные стороны функционирования объекта и при перемещении центра внимания исследователя рассмотренные ранее подсистемы переходят во внешнюю среду. Иерархическая структура моделей может раскрывать и ту последовательность, в которой изучается реальный объект, а именно: последовательность перехода от структурного (топологического) уровня к функциональному (алгоритмическому) и от функционального к параметрическому.

Результат моделирования в значительной степени зависит от адекватности исходной концептуальной (описательной) модели, от полученной степени подобия описания реального объекта, числа реализаций модели и многих других факторов. Применение ЭВМ позволяет исследовать имитационную модель 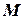, задаваемую в виде определенной совокупности отдельных блочных моделей и связей между ними, физико-статистических моделей, полученных на ранних стадиях математического моделирования, в их взаимодействии в пространстве и времени при реализации какого-либо процесса, что в совокупности составляет имитационную систему. Можно выделить три основные группы блоков: блоки, характеризующие моделируемый процесс функционирования системы 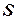; блоки, отражающие внешнюю среду 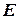и ее воздействие на реализуемый процесс; блоки, играющие служебную вспомогательную роль, обеспечивая взаимодействие первых двух, а также выполняющие дополнительные функции по получению и обработке результатов моделирования. Кроме того, имитационная система характеризуется набором переменных, с помощью которых удается управлять изучаемым процессом, и набором начальных условий, когда можно изменять условия проведения машинного эксперимента.

Как вытекает из изложенного, математическое моделирование представляет собой довольно сложный многоплановый процесс, который должен иметь определённое обеспечение (аналогично процессу САПР). В общем случае имитационная система моделирования как одна из наиболее сложных характеризуется следующими видами обеспечения :

· Математическое обеспечение включает в себя совокупность математических соотношений, описывающих поведение реального объекта, совокупность алгоритмов, обеспечивающих как подготовку, так и работу с моделью. Сюда могут быть отнесены алгоритмы ввода исходных данных, имитации, вывода, обработки.

· Программное обеспечение по своему содержанию включает в себя совокупность программ: планирования эксперимента, построения имитационной модели, проведения машинного эксперимента над имитационной моделью, обработки и интерпретации его результатов. Кроме того, программное обеспечение имитационной системы должно обеспечивать синхронизацию процессов в модели, т.е. необходим блок, организующий псевдопараллельное выполнение процессов в модели. Машинные эксперименты с имитационными моделями не могут проходить без хорошо разработанного и реализованного информационного обеспечения.

· Информационное обеспечениевключает в себя средства и технологию организации и реорганизации базы данных моделирования, методы логической и физической организации массивов, формы документов, описывающих процесс моделирования и его результаты. Информационное обеспечение имитационной системы является наименее разработанной частью, поскольку только в настоящее время наблюдается переход к созданию сложных имитационных моделей и разрабатывается методология их использования при анализе и синтезе сложных систем с использованием концепции базы данных и знаний.

· Техническое обеспечение имитационной системы включает в себя прежде всего средства вычислительной техники, связи и обмена между оператором и сетью ЭВМ, ввода и вывода информации, управления проведением эксперимента. К техническому обеспечению предъявляются весьма серьёзные требования по надежности функционирования, так как сбои и отказы технических средств, ошибки оператора ЭВМ могут резко увеличить время работы с имитационной моделью и даже привести к неверным конечным результатам.

· Организационно-методическое обеспечение имитационной системы представляет собой совокупность научных и прикладных методик и методов, а также нормативно-технических и организационно-методических документов и мероприятий, используемых на всех этапах взаимодействия человека-экспериментатора с инструментальными средствами (ЭВМ, гибридными комплексами и т.д.). Эти документы, используемые на всех стадиях разработки и эксплуатации имитационных систем и их элементов, предназначены для формирования и поддержания эргономического качества путём обоснования и выбора организационно-проектных решений, которые создают оптимальные условия для высокоэффективной деятельности человека во взаимодействии с моделирующим комплексом.

Необходимо помнить, что даже при всем совершенстве средств вычислительной техники, которые в настоящее время широко используются либо для вычислений при аналитическом моделировании, либо для реализации имитационной модели системы, могут лишь помочь с точки зрения эффективности реализации сложной модели, они не позволяют подтвердить правильность той или иной модели. Только на основе обработанных данных, опыта исследователя можно с достоверностью оценить адекватность модели по отношению к реальному процессу.

Разработка теоретических моделей исследования качества изделий, технологических процессов, средств и систем машиностроительных производств

Без преувеличения можно отметить, что определяющая роль в построении математических моделей технических систем принадлежит математическим методам при рациональном их применении. Наряду с аналитическими методами анализа непрерывных процессов, дифференциальным и интегральным исчислением, широкое применение находят методы дискретной математики (теории множеств, графов и др.), на которых базируются теоретические основы систем автоматизированного проектирования (САПР), автоматизированные системы управления технологическими процессами (АСУ ТП), автоматизированные системы управления производством (АСУП) и сопутствующих компонент, включающих решение важных научно-технических задач. Вопросы идентификации технических и организационных систем и их составляющих, построение физико-статистических моделей процессов при наличии случайных параметров, протекающих в технологических системах, их имитационное моделирование решаются на базе теории вероятностей, теории случайных функций, математической статистики и теории планирования эксперимента.

Важным в процессе математического моделирования при реализации его результатов на практике, особенно при условии их многовариантности, что характерно для технологии машиностроения, является знание и правильное применение теории принятия решений, базирующейся на теории игр и теории массового обслуживания.

Большую роль в моделировании и проектировании технологических процессов производства играет описательный способ задания множеств оборудования, инструмента, операций, поверхностей, физических процессов и др. Он связывает учение о множествах с учением о высказываниях, составляющее часть математической логики, которая обеспечивает математически строгое логическое описание, синтез и рациональный выбор как самого технологического процесса, так и его компонент.

Практически на всех этапах математического моделирования приходится оперировать с матрицами, особенно в системах построения физико-статистических моделей методами корреляционно-регрессионного анализа, планирования эксперимента и нейросетевого моделирования.

Что же представляет собой математический аппарат инженера?

Математический аппарат инженера определяется как взаимосвязанная совокупность языка, методов математики и моделей, ориентированная на решение инженерных задач.

В формальный язык математики и ее разделов входят системы символов, обозначающие математические объекты и переменные, а также операции над объектами и отношения между ними.

Так, различные типы геометрии классифицированы Феликсом Клейном в соответствии с теми свойствами фигур, которые остаются неизменными, когда они подвергаются разнообразным группам преобразований.

Эвклидова геометрия изучает такие объекты как углы, которые сохраняются при повороте, переносе, сжатии, растяжении. В афинной геометрии отношение коллинеарных отрезков постоянно 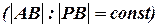. В проективной геометрии инвариантно перекрестное отношение коллинеарных отрезков 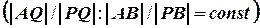. Топология изучает свойства, сохраняющиеся при изгибах, сжатиях, растяжениях, кручении. Порядок следования точек при таких деформациях сохраняется. 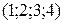В теории точечных множеств рассеянные точки сохраняют нумерацию , совпадающую с нумерацией точек исходной фигуры. Теория точечных множеств в широком смысле может быть представлена как изучение свойств, сохраняющихся при взаимно однозначных преобразованиях.

В соответствии с этим в технических задачах может быть использован различный формальный язык математики. Так, при моделировании процессов термомеханической обработки при рассмотрении упругости и пластичности обрабатываемого материала целесообразно использовать Эвклидову и аффинную геометрию, при описании пластичности и вязкости среды– переходить от афинной геометрии к топологии. В процессах ионно-лучевой обработки рационально использовать проективную геометрию при лучевых процессах, а теорию точечных множеств – при воздействии частицами.

 

 

 

 

Рис. Эвклидова геометрия, включающая:

а – параллельный перенос; б – поворот; в – равномерное сжатие и растяжение