Классификация моделей по типам

На основе силовых полупроводниковых приборов (СПП) созданы электрические аппараты постоянного и переменного тока различного назначения: контакторы, пускатели, автоматические выключатели, регуляторы тока и напряжения и др. По многим характеристика они превосходят свои контактные аналоги. В частности, полупроводниковые аппараты имеют значительно более высокое быстродействие. Вследствие отсутствия подвижных частей и дуговых явлений им присущи относительно низкие эксплуатационные расходы и повышенных коммутационный ресурс. Отсутствуют также такие явления, как дребезг и сваривание контактов, характерные для электромеханических аппаратов. Все это обусловило широкое использование полупроводниковых аппаратов в автоматизированном электроприводе, сетях электроснабжения, системах автоматизации производственных процессов.

Коммутационные устройства переменного тока на основе СПП могут быть выполнены по различным схемам. Некоторые из них, наиболее часто применяемые в практике, приведены на рис. 1.

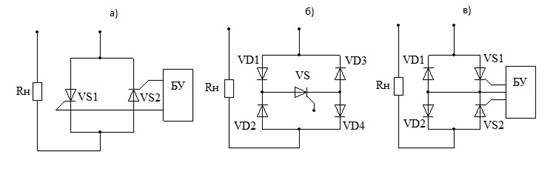
Рис. 1 Принципиальные схемы полупроводниковых аппаратов переменного тока

Первая схема (рис. 1, а) является основным вариантом исполнения силового блока коммутирующих аппаратов переменного тока. В ней используются два встречно-параллельно соединенных тиристора, каждый из которых может проводить ток лишь в одном направлении. Поочередное включение тиристоров в соответствии с изменением полярности напряжения сети обеспечивает прохождение синусоидального тока в нагрузке.

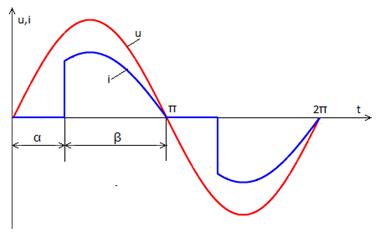В конце каждого полупериода при снижении мгновенного значения тока нагрузки до величины, называемой током удержания, тиристор выключается. Очевидно, что для поддержания аппарата во включенном состоянии на входы тиристоров периодически, со сдвигом 180 градусов, должны подаваться импульсы напряжения, синхронизированные с напряжением сети или током в нагрузке. Эту функцию выполняет блок управления контактора (БУ). Также с помощью БУ можно осуществить задержку выдачи управляющих импульсов на тиристоры на некоторый угол α по отношению к нулевому значению питающего напряжения (рис. 2). Тиристоры в этом случае будут находиться во включенном состоянии лишь часть полупериода, называемою углом проводимости β. Изменением угла задержки включения, что соответствует изменению угла проводимости тиристоров, обеспечивается регулирование в нагрузке средних значений тока и напряжения. В результате, кроме выполнения функций коммутирования цепей, тиристорный контактор переменного тока способен осуществить регулирование напряжения и тока.

Коммутирующие устройства, выполненные по схемам рис. 1, б, в, сочетают в себе тиристоры и диоды. По принципу действия и выполняемым функциям они аналогичны рассмотренному выше устройству. Однако такое построение силовых блоков позволяет существенно упростить систему управления ими (БУ), так как в обоих случаях требуется лишь один источник управляющих импульсов. В работе используется схема, приведенная на рис. 1 в. Полная схема лабораторной установки приведена на рис. 3.

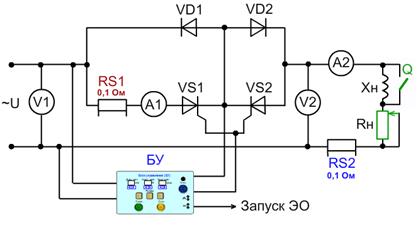
^{Рис. 3. Схема лабораторной установки}

Зависимость среднего тока через тиристор определяется по формуле:

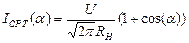
Зависимость действующего тока через тиристор определяется по формуле:

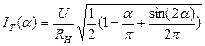
α - угол задержки включения тиристоров;

U - действующее значение напряжения сети;

R_н - нагрузка контактора;

Зависимость действующего тока и напряжения в нагрузке при различных углах проводимости рассчитываются соответственно по формулам:

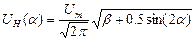
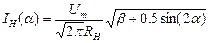
U_m - амплитудное значение напряжения;

При активно-индуктивной нагрузке форма тока в цепи не повторяет форму напряжения, так как возникает ЭДС самоиндукции, препятствующая нарастанию и спаданию тока. Поэтому ток через тиристор протекает в течение некоторого времени после изменения знака питающего напряжения.

Закон изменения тока тиристора, проводящего в положительный полупериод, можно получить, решив дифференциальное уравнение

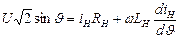
Это уравнение справедливо в интервале α≤ϑ≤α_выкл, вне которого i_H=0 (α_выкл – угол выключения тиристора).

Решение для тока

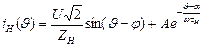
Где φ=arctg(ωL_H/R_H);

τ_H=L_H/R_H;

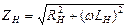
А - постоянная интегрирования, которая определяется из условия, что при ϑ=α, i_H=0.

Выражение для тока нагрузки, а следовательно и для тока тиристора

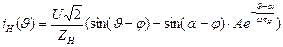
Угол выключения тиристора α_выкл может быть определен из трансцендентного уравнения

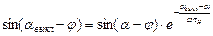
которое получается из уравнения приведенного выше, при условии i=0 при ϑ=α_выкл=α+β. Результаты решения представлены на рис. 4.

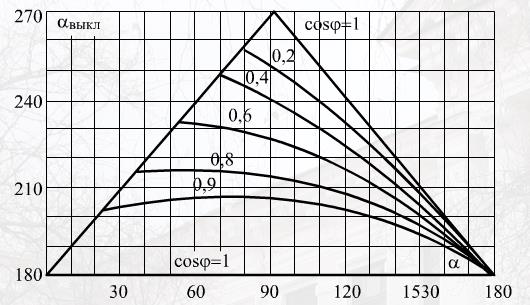
Рис. 4 Связь угла управления с углом выключения при активно-индуктивной нагрузке

При α=φ свободная составляющая тока не возникает, и ток определяется только принужденной составляющей. Этот угол управления называется критическим α_кр, т.к. конец импульса тока через один тиристор совпадает с началом тока через второй. При α>α_кр ток нагрузки носит прерывистый характер, а при α<α_кр – непрерывный. Т.е. регулирование напряжения и тока нагрузки возможно только при изменении угла управления тиристоров в пределах α_кр<α<π.

Действующее значение тока тиристора определяется из выражения

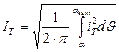
А среднее значение – из выражения

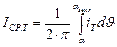
Действующее значение напряжения в нагрузке

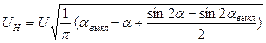
Классификация моделей по типам

Рассмотрим их краткие характеристики и главные отличительные особенности.

1.Материальные (реже – вещественные, действующие, наглядные) модели – это некоторые материальные объекты или совокупность объектов, отражающие в той или иной степени свойства объекта моделирования. В зависимости от полноты и способа отражения этих свойств материальные модели подразделяются на три основных типа:

· геометрическиемодели – представляют некоторый объект, геометрически подобный своему оригиналу, и дают внешнее представление об оригинале. Выполняются как в натуральную величину (модели отливок и др.), так и в уменьшенном масштабе (модель нового автомобиля, демонстрационная модель детали или агрегата машины и т.д.).

· физические модели – отражают подобие между оригиналом и моделью не только с точки зрения их формы и геометрических соотношений, но и с позиций происходящих основных физических процессов. Необходимо помнить и всегда иметь в виду, что физически подобными называются явления в геометрически подобных системах, в процессе функционирования которых отношения характеризующих их физических величин в сходственных точках составляют постоянную величину. При физическом моделировании модель и объект моделирования всегда должны иметь одинаковую физическую природу. При изменении геометрических параметров при переходе от объекта-оригинала к модели должны соответственно изменяться и другие физические параметры, являющиеся входными или возбуждающими воздействиями.

Предметно-математическиемодели – предполагается лишь тождественность математического описания процессов в оригинале и модели (требование тождественности их физической природы снимается), хотя эти процессы и могут развиваться на совершенно различной материальной основе. В этом случае предметно-математическая модель представляет материальную систему, в которой происходят иные физические процессы, чем в оригинале, но и те, и другие могут быть описаны одинаковыми или подобными математическими выражениями.

2.Идеальные модели (абстрактные концептуальные) включают модели двух типов:

· мысленные (умозрительные, интуитивные) – существуют в мыслях человека, воображаются человеком.

· логико-математические (формальные, знаковые, математи­ческие) – представляют собой воплощение мысленных моделей в форму различных математических выражений (системы уравнений или неравенств с буквенными или численными коэффициентами, логические выражения, таблицы, матрицы, схемы, графики и др.) и других способов логического и математического описания исследуемых явлений и процессов. В принципе это не что иное, как математические модели.

В группе математических моделей, в свою очередь, выделяются подгруппы:

А. Модели прямой аналогии, в которых каждой физической величине оригинала сопоставляется в модели величина другого рода, изменяющаяся в пространстве и во времени сходным образом.

Б. Структурные или операционные модели, в которых математическое описание оригинала воспроизводят в виде совокупности отдельных операций, выполняемых соответствующими блоками.

В. Цифровые модели, в которых те же операции выполняются в цифровом виде, обычно последовательно одна за другой в общем процессоре.

Г. Функциональные модели, в которых воспроизводится только поведение, функция оригинала, но не его устройство, так что по описанию модель может быть не подобна натуре.

В машиностроении в последнее время широко используются относительно новые типы математических моделей:

· физико-аналитические модели – представляют собой аналитические зависимости между входными факторами и выходными параметрами технологических и иных систем, полученные на основе анализа реально протекающих физических процессов и их аналитических описаний.

Наиболее ярким примером могут служить модели формирования параметров качества поверхностного слоя и процессов контактирования шероховатых поверхностей.

· физико-статистические модели – представляют собой зависимости между входными параметрами технологических и иных систем, полученные статистическими методами (методами планирования эксперимента, множественного корреляционно- регрессионного анализа и др.), но факторы, включённые в исследование, имеют четкий физический смысл и являются реальными технологическими переменными. Такие модели не следует относить к типу эмпирических, так как они строятся на базе активного, а не пассивного эксперимента, т.е. с использованием кибернетического подхода, и не представляют собой процесс сглаживания результатов пассивных наблюдений, который осуществляется подбором подходящего уравнения, включающего то или иное число независимых переменных, не несущих на себе никакой нагрузки с точки зрения физики протекающих в реальной системе процессов. Такие модели строятся в том случае, когда физику протекающих процессов аналитически описать не представляется возможным. Однако на их основе возможно с достаточной надёжностью прогнозировать параметры качества поверхностного слоя (КПС) обрабатываемых деталей и др., формируемые в ходе обработки при заданных условиях, а также осуществлять процесс управления технологической системой, обеспечивающий получение параметров качества обработки в допустимых пределах с заданной надёжностью.

В общем случае математические модели связывают входные (независимые) переменные 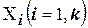исследуемого процесса, называемые входными факторами, или воздействиями, с выходными (зависимыми) характеристиками 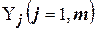, которые обычно именуют функциями отклика (например, в технологических системах это параметры точности обработки, качества поверхностного слоя; энергозатраты, производительность и др.). Такие уравнения связи имеют вид:

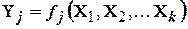
Модели, отображающие случайный (стохастический) характер параметров и факторов системы, называются статистическими, или стохастическими в отличие от детерминированных, не учитывающих вероятностных характеристик процессов.

По мере уменьшения величины параметров 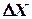и 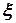уравнение приближается по структуре к уравнению, описывающему детерминированные системы.

Обычно детерминированные модели, представляющие собой систему уравнений, удается составить только в тех случаях, когда о процессах в описываемой системе имеются ясные физические представления и эти представления можно формализировать. В таких случаях говорят, что система представляет собой «белый ящик» – объект с известной структурой и функциями.

Однако получаемая таким образом модель может оказаться громоздкой, а ее информационное обеспечение весьма трудоемким. Поэтому часто используют статистические модели для описания детерминированных систем. В таких случаях рассматривают систему как «черный ящик» с неизвестной структурой, в котором доступны для изучения только контролируемые входные параметры 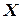и измеримые выходные характеристики 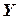. Получив таблицу соответствий { 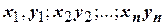}, принимают их за случайную выборку из генеральной статистической совокупности { 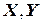}. Полученная статистическая модель при соответствующей интерпретации результатов позволяет раскрыть механизм, сделать «белыми» некоторые части устройства и функционирования «черного ящика».

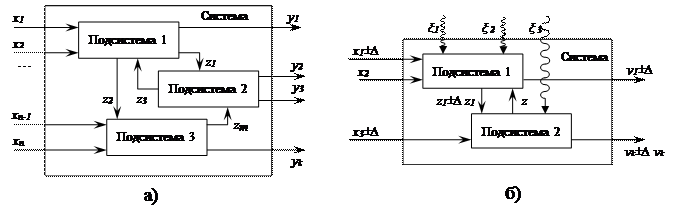Схемы моделей производственных систем при наличии в них детерминированных (а) и стохастических (б) процессов

Детерминированные модели могут также использоваться для описания стохастических систем, если объектом изучения являются их усредненные характеристики. Таким образом, статистические модели – это более широкий класс моделей, включающих детерминированные модели как предельный частный случай, в котором выходные параметры 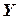однозначно определяются входными переменными .

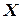Если доказано подобие натурных и моделирующих процессов, то можно говорить об адекватности моделей.

В зависимости от характера и пространственной структуры описываемых систем различаются модели с распределенными и сосредоточенными параметрами. В связи с различной интенсивностью моделируемых процессов во времени различают статические модели, описывающие установившиеся процессы вблизи состояния равновесия; стационарные модели, характеризуемые постоянством основных параметров во времени; динамические модели систем, в которых входной переменной процесса является время.

В зависимости от конкретного вида применяемого математического аппарата различают модели матричные, сетевые, дифференциальные, интегральные, алгоритмические, программные и др.

Кроме изложенной классификации моделей по типу, существует часто используемый вид классификации моделей по назначению. В этом плане их можно разбить на следующие:

1. Информационные (описательные), используемые в качестве обучающих или советующих систем, для изучения взаимного влияния факторов на выходные параметры, установления границ, в пределах которых достигается рациональный режим работы системы и т.д.

2. Оптимизационные, используемые для поиска оптимальных условий протекания процесса в системе. В качестве оптимизационных могут применяться информационные модели, дополненные блоком оценки результата на основании целевой функции, с учетом налагаемых ограничений на изменение входных и выходных переменных.

3. Управления (регулирования) процессом, используемые для воздействия на систему в реальном масштабе времени с целью компенсации нежелательных случайных возмущений и смещения системы в направлении экстремального значения целевой функции. Такая модель может служить компонентом системы автоматического управления (регулирования).

4. Эвристические, используемые для получения новых знаний и изучения механизма процессов на основе сопоставления результатов моделирования и натурных измерений, выдвижения и проверки новых гипотез о структуре взаимосвязей между факторами, введения дополнительных факторов в модель и т.д.