Элементы теории множеств и ее применение в моделировании технических систем.
Понятие множества является одним из фундаментальных понятий математики, которые трудно определяются через элементарные понятия. Одним из наиболее распространенных его определений является следующее:
Множество– совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое.
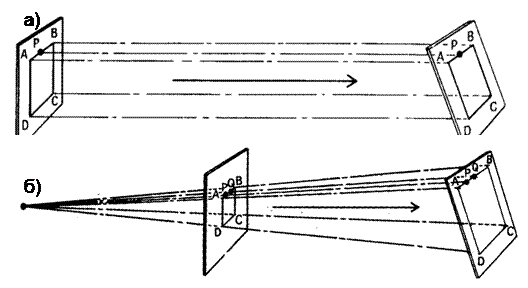 |
Афинная геометрия (а) с параллельным проецированием, проективная геометрия (б) с проецированием от точечного источника
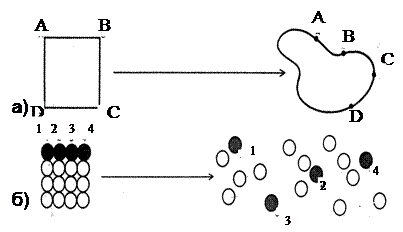
Топология (а), содержащая неразрывную деформацию, и теория точечных множеств (б), описывающая рассеяние
Приведем примеры множеств: множество оборудования механообраба-тывающего цеха, множество деталей, множество возможных вариантов технологического процесса обработки, множества инструмента, операций, персонала и т.д.
Отдельные объекты представляют собой элементы множества, которое обозначается парой фигурных скобок { }. Для конкретных множеств с этой целью используются различные прописные буквы 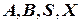 или прописные буквы с индексами:
или прописные буквы с индексами: 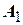 ,
, 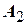 , …. Элементы множества обозначаются различными строчными буквами
, …. Элементы множества обозначаются различными строчными буквами 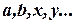 или строчными буквами с индексами
или строчными буквами с индексами 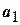 ,
,  …. Используются символы принадлежности
…. Используются символы принадлежности 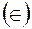 и непринадлежности (
и непринадлежности ( 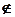 или
или 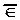 ) элемента или элементов множеству:
) элемента или элементов множеству:
· 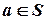 – элемент
– элемент 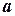 принадлежит множеству
принадлежит множеству 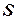 или
или 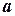 является элементом множества
является элементом множества 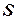 ;
;
· 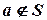 (или
(или 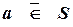 ) – элемент
) – элемент 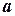 не является элементом множества
не является элементом множества 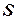 (элемент
(элемент 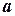 не принадлежит множеству
не принадлежит множеству 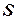 ).
).
Вместо записи 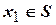 ,
, 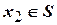 , …,
, …, 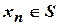 с целью сокращения можно использовать запись
с целью сокращения можно использовать запись 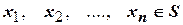 .
.
Множество конечное, если количество его элементов представляет собой натуральное конечное число 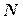 , и бесконечное, если оно содержит бесконечное число элементов
, и бесконечное, если оно содержит бесконечное число элементов 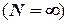 .
.
Существует два способа задания множеств: перечисление и описание. Задание множества способом перечисления соответствует перечислению всех элементов, составляющих множество. Такой способ удобен при рассмотрении конечных множеств, содержащих небольшое число элементов, но иногда он может применяться и для задания бесконечных множеств, например 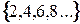 . Естественно, что такая запись применима, если вполне ясно, что понимается под многоточием.
. Естественно, что такая запись применима, если вполне ясно, что понимается под многоточием.
Отдельный способ задания множества состоит в том, что указываются все элементы множества.
Если 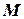 количество станков в цехе, то множество
количество станков в цехе, то множество 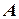 токарных станков запишется в виде:
токарных станков запишется в виде:
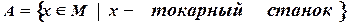 .
.
Читается: множество 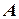 состоит из элементов
состоит из элементов 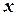 множества
множества 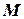 , обладающих тем свойством, что
, обладающих тем свойством, что 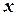 является токарным станком. В случаях, когда ясно, из какого множества берутся элементы
является токарным станком. В случаях, когда ясно, из какого множества берутся элементы 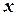 , указания о принадлежности
, указания о принадлежности 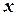 к множеству
к множеству 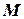 можно не делать:
можно не делать:
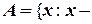 проходной резец},
проходной резец},
 .
.
В первом случае ясно, что элементы 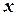 принадлежат к множеству резцов, а во втором – к множеству решений уравнения
принадлежат к множеству резцов, а во втором – к множеству решений уравнения 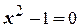 , т.е. к множеству
, т.е. к множеству 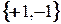 .
.
Если 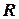 – множество целых чисел, то
– множество целых чисел, то 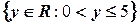 – множество
– множество 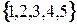 .
.
Пустым множеством (Æ) называется множество, не содержащее ни одного элемента.
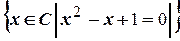 =Æ, так как уравнение не имеет вещественных решений.
=Æ, так как уравнение не имеет вещественных решений.
Пустое множество будем условно относить к конечным множествам.
Два множества называют равными, если они состоят из одних и тех же элементов.
Множества 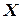 и
и 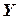 не равны
не равны 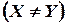 , если либо в множестве
, если либо в множестве 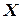 есть элементы, не принадлежащие
есть элементы, не принадлежащие 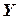 , либо в множестве
, либо в множестве 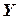 есть элементы, не принадлежащие
есть элементы, не принадлежащие 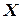 .
.
Символу равенства множеств присущи свойства:
· 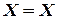 – рефлексивность;
– рефлексивность;
· если 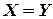 , то
, то 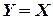 – симметричность;
– симметричность;
· если 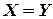 и
и  , то
, то 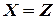 – транзитивность.
– транзитивность.
Из определения равенств множеств вытекает, что порядок элементов в множестве несуществен:
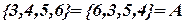 .
.
Из определения множества следует, что в нем не должно быть неразличимых элементов. Запись 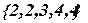 следует заменить
следует заменить 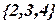 , т.к. в первом случае наблюдается повторение одних и тех же элементов.
, т.к. в первом случае наблюдается повторение одних и тех же элементов.
Множество 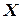 является подмножеством множества
является подмножеством множества 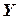 , если любой элемент множества
, если любой элемент множества 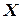 является элементом множества
является элементом множества 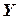 .
.
Для определения подмножества используются символы:
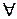 – квантор, означает «любой», «каков бы ни был», «для всех».
– квантор, означает «любой», «каков бы ни был», «для всех».
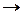 – символ следствия (импликации), означающий «влечет за собой».
– символ следствия (импликации), означающий «влечет за собой».
Определение подмножества:
Для любого 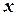 утверждение «
утверждение « 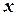 принадлежит
принадлежит 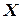 »влечет за собой утверждение «
»влечет за собой утверждение « 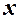 принадлежит
принадлежит 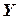 »запишется в виде:
»запишется в виде:
" 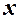 [
[ 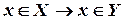 ]
]
кратко: 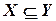 обозначает, что
обозначает, что 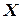 является подмножеством
является подмножеством 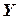 или
или 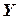 ,содержащий
,содержащий 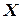 .
.
Если 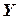 содержит и другие элементы, кроме элементов из
содержит и другие элементы, кроме элементов из 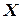 , то используют символ
, то используют символ 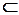 – строгое включение:
– строгое включение: 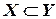 . Связь между символами
. Связь между символами  :
:
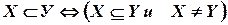
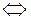 – обозначение эквивалентности «то же самое, что».
– обозначение эквивалентности «то же самое, что».
Свойства подмножеств:
· 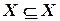 – рефлексивность
– рефлексивность
· 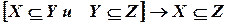 – транзитивность.
– транзитивность.
Всегда можно считать, что любое множество 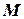 содержит в себе в качестве подмножества пустое множество: Æ
содержит в себе в качестве подмножества пустое множество: Æ 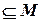 .
.
Часто возникающая задача определения наибольшего или наименьшего элемента множества для конечных множеств не представляет труда, но для бесконечных положение может быть иным
Пусть 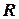 – множество всех вещественных чисел, а
– множество всех вещественных чисел, а 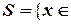
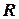
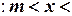
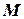 }. Множество
}. Множество 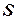 представляет собой незамкнутый отрезок вещественной оси и не имеет наибольшего и наименьшего элементов. Однако можно говорить о границах такого множества, понимая под ними числа
представляет собой незамкнутый отрезок вещественной оси и не имеет наибольшего и наименьшего элементов. Однако можно говорить о границах такого множества, понимая под ними числа 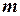 и
и 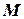 , дополняющие множество
, дополняющие множество 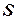 до замкнутого отрезка. При этом точка
до замкнутого отрезка. При этом точка 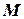 называется верхней границей множества
называется верхней границей множества 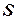 ,или супремумом, и обозначается
,или супремумом, и обозначается 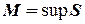 , а точка
, а точка 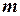 называется нижней границей множества
называется нижней границей множества 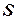 ,или инфинумом, и обозначается
,или инфинумом, и обозначается 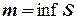 .
.
Согласно теореме о верхней и нижней границах подмножества можно утверждать:
если 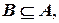 то
то 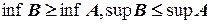 .
.
Действия над множествами во многом напоминают действия сложения и умножения в элементарной алгебре. Вспомним основные ее законы.
Пусть 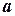 и
и 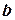 – некоторые числа, (
– некоторые числа, ( 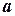 +
+ 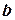 )– их сумма и (
)– их сумма и ( 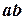 )– их произведение. Сумма и произведение чисел обладают следующими свойствами, называемыми законами алгебры:
)– их произведение. Сумма и произведение чисел обладают следующими свойствами, называемыми законами алгебры:
1. 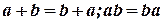 – коммутативный или переместительный закон;
– коммутативный или переместительный закон;
2. 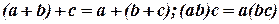 – ассоциативный или сочетательный закон;
– ассоциативный или сочетательный закон;
3. 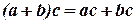 – дистрибутивный или распределительный закон.
– дистрибутивный или распределительный закон.
В ассоциативном и коммутативном законах можно заменить действие сложения умножением, а действие умножения сложением. Однако в дистрибутивном законе подобной симметрии нет. Если в этом законе заменить сложение умножением, а умножение сложением, то придем к абсурду:
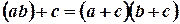 .
.
В отличие от элементарной алгебры в алгебре множеств все три закона симметричны относительно действий сложения и умножения.
Рассмотрим числа 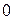 и
и 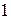 . Это замечательные числа! Прибавление первого и умножение на второе не меняет ни одного числа:
. Это замечательные числа! Прибавление первого и умножение на второе не меняет ни одного числа:
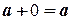 ,
, 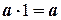 .
.
Второе соотношение получено из первого заменой  на
на 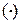 и
и 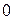 на
на 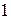 . Но число
. Но число 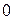 играет особую роль по сравнению со всеми другими числами, в том числе и с единицей. Это вытекает из соотношения
играет особую роль по сравнению со всеми другими числами, в том числе и с единицей. Это вытекает из соотношения 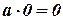 . Если заменим здесь
. Если заменим здесь 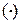 на
на  и
и 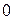 на
на 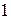 , то получим соотношение
, то получим соотношение 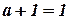 , которое почти никогда не будет верным. В алгебре множеств сходство между нулем и единицей значительно большее, чем в обычной алгебре.
, которое почти никогда не будет верным. В алгебре множеств сходство между нулем и единицей значительно большее, чем в обычной алгебре.
Теория множеств, являясь фундаментом, в свою очередь, получает дальнейшее развитие в таком разделе математики, как высшая алгебра.
Правила выполнения алгебраических действий (сложение, умножение, деление) для различных объектов (рациональные и комплексные числа, векторы, матрицы и т.п.) различны. Однако эти действия имеют общие свойства, значение которых позволяет установить возможность или невозможность применения этих действий для конкретного класса объектов, составляющих множества. Установление этих свойств приводит к понятиям алгебраической операции, группы, кольца, поля.
Дата добавления: 2015-04-03; просмотров: 1525;
