Технологиялық үдерістер мен механикаландыру құралдарының математикалық моделін қалыптастыру

Теориялық зерттеу көбінесе қайшылық формасында типі мен күрделілік деңгейі бойынша әртүрлі тапсырмаларды шешу мен үздіксіз қоюдан тұрады. Кез келген тапсырманың шарты мен талабы болады. Шарт – тапсырманы орындау кезінде басшылыққа алынатын, ақпараттық жүйе анықтамасы. Талап – тапсырманы орындау үдерісінде қол жеткізуге ұмтылу керек мақсат. Шарт пен талап бастапқы, тартылған және шығыс болуы мүмкін. Бастапқы шарт тапсырманың алғашқы қойылуында орын алады. Тапсырманы шешу үшін мұндай шарттар жеткіліксіз болған жағдайда жаңа деректер тартылады, оларды – тартылған шарттар деп атайды. Деректердің үшінші деңгейі – шығыс – бұл тапсырманы шешу барысында табу қажет болатын деректер.

Тапсырманың шарты мен талабы қайшылықта болады, олар бірнеше рет қақтығысады, салыстырылады, ақыр соңында бір-біріне жақындасады. Тапсырманың құрылымдық компоненттерінің мұндай түрленуі қойылған тапсырма шешілмейінше жалғасын табады.

Теориялық зерттеу табиғаттың түрлі салаларын ашу, тексеру, ішінара меңгеруден, дүниетанымды қалыптастыру және дамытудан тұратын ойлау функциясы болып табылады.

Жалпы практикалық тапсырманы математикалық әдіспаен шешу кезегімен орындалады: математикалық үлгіні әзірлеу; алынған үлгіні зерттеу әдісін таңдау; математикалық зерттеу нәтижелерін талдау.

Ауылшаруашылық өндірісті механикаландыру құралдарының қызметінің зерттелетін үдерісінің математикалық үлгісі математикалық қатынасты, көбінесе, параметрлер мен үдеріс режимдерінің өзара байланысын білдіретін, осы үдерісті не оның жекелеген бөліктерін сипаттайтын математикалық теңдеулердің тұтас жүйесін білдіреді. Зерттеу нысанының түріне байланысты үдеріс не құбылысты математикалық сипаттау үздіксіз немесе дискретті, детерминделген немесе стохастикалық формада болуы мүмкін. Математикалық үлгілеуде басты және оның алғашқы кезеңі болып нысанды анықтау, зерттеу мақсаты мен міндеттерін қою, критерийлерді таңдау және оларды басқару табылады.

Математикалық үлгілеудің алғашқы кезеңіндегі әрекеттер тізімінде нысанның сыртқы шектесетін нысандармен өзара әрекеті саласындағы қызмет ету орнына сәйкес саналы шектеулер енгізу маңызды болып табылады. Бұл шектеулер (нысанның әсер ету саласының шекарасы) келесі шарттар бойынша белгіленеді:

- шекаралар зерттеу нысанына әсері нөлге тең емес элементтерді қамтуы керек;

- зерттеу нысанының шекара сыртындағы басқа нысандармен өзара әсері нөлге жақындайды.

Математикалық үлгілеу үдерісінде нақты шектеулер орнату осы үлгіге енгізілген факторлардың маңыздылығы мен оны сыртқы ортадан тәуелсіз тұйықталған жүйеде қарау мүмкіндігін негіздейді. Әрине, бұл шешімдердің барлығы да белгілі бір деңгейде жақындықпен орындалады.

Математикалық үлгі типін және оны құру үшін математикалық аппаратты таңдау – үлгілеу жолымен теориялық зерттеудің келесі кезеңі, осыған байланысты, алдымен, зерттеу нысаны қандай типке: сызықты немесе сызықсыз; динамикалық немесе статикалық; детерминдерген немесе стохастикалық; стационарлық немесе стационарлық емес типке жататыны анықталады (сурет 3.1).

Зерттеу нысаны алдын ала талдау және оның жалпы сипаттамасы туралы қорытынды математикалық үлгі құру үшін математикалық аппаратты нақты таңдау мүмкіндігін негіздейді.

Математикалық апаратты таңдау бір мәнді еместігін, сондай-ақ нысан сипаттамасы да қатаң шекарамен шектелмегенін ескеру керек. Сондықтан, 3.1 суреттегі сызбаны басшылыққа алып, детерминделген динамикалық үдеріс сипаттамасын диффыеренциалды және интегралды теңдеулер, туынды, сызықты және сызықсық алгебра теңдеулерінің көмегімен іске асыруға болады. Стохастикалық стационарлық үдерістердің математикалық үлгілерін құру үшін ықтималдылық теориясы, информация, алгебра теориясы жеткілікті. Стационарлық емес үдерістер үшін кездейсоқтық теориясын, марков үдерісінң, ықтималды сипаттамалы дифференциалды теңдеуді т.б. меңгеріп, қолдану керек.

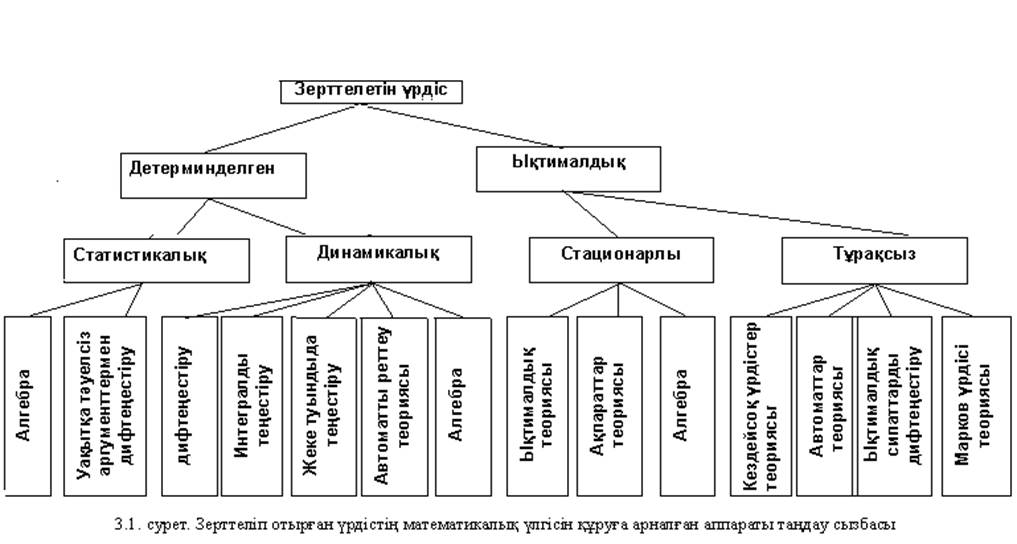
Зерттеудің анықтығы деңгейін арттыру үшін нысандар қатарын математикалық үлгісін тек қана заңға сәйкес анықталатын коэффициентті дифференциалды теңестіру теориясын қолдана отырып құруға болатын ықтималды- детерминирленген тобына бөледі.

Үрдістің сызықтығы зерттеліп отырған нысанға сыртқы әсердің көлемі мен оның сыртқы орта әсеріне ең жоғарғы әрекеті арасындағы байланысы сипатына қарай белгіленеді, басқа сөзбен айтқанда шығыс және кіріс дабылдарының көлемдерінің арасындағы сипат бойынша белгіленеді. Осыған байланысты, зерттеліп отырған нысанның статистикалық сипатының сызықтығы кезінде ол желілік функцияларды қолдану арқылы модельденеді.

Сызықсыз математикалық модель сызықсыз статистикалық сипатты нысанды суреттеу үшін және нысанның сыртқы ауытқуға кеш әрекет ету дерегі анықталған кезде қолданылады.

Нысанның динамикалығы немесе статистикалығы параметрлердің мағыналарының уақыт бойынша өзгеру сипатына қарай анықталады.

Детерминирленген үрдістің статистикалығы немесе динамикалығы туралы оның шығыс сипатына қарай пікір айтуға болады.

Егер дабылдың орташа арифметикалық мағынасы уақыттың әртүрлі бөліктері бойынша зерттеліп отырған көрсеткішті өлшеу тәсілінің дәлдігімен белгіленген мүмкін шектіктен шықпаса, онда бұл жағдай үрдістің статикалығын көрсетеді. Ықтимал үрдістердің (нысандар) статистикалық белгісі болып қатысты ұйымның деңгейінің өзгеру шектігін аспауы болып табылады. Бұл жағдайда үлгі түрі нысанның стационарлы үрдіс класына қатыстылығымен анықталады. Стационарлы үрдістерге орташа арифметикалық ауытқулары төмендегідей болатын үрдістер жатады:

(М·τ_min +∆Х) > М·τ_i > (М·τ_min - ∆Х)

Мұнда М·τ_min - ең төменгі орташа арифметикалық ауытқу (осы үрдісті іске асыру қатарынан);

∆Х – үрдіс параметрін өлшеу дәлдігі;

Мысалы, орташа арифметикалық ауытқумен бес көрсеткіш алынды М·τ_min1 = 24; М·τ_min2=24,5; М·τ_min3=24,7; М·τ_min4=23,5; М·τ_min5=23,00

Өлшеу дәлдігі ∆Х=1,8, М·τ_min = 23,00

Орташа арифметикалық ауытқу бойынша үрдіс (3.1.) шарт орындалатындықтан стационарлы:

(23,00 +1,8) > М·τ_i > (23,00 - 1,8)

24,8 > М·τ_i > 21,2

Нысанның (процесстің, құбылыстың) стационарлығы шаршылы ауытқу бойынша ұқсас белгіленеді.

Оның құрылуына көмек беретін үлгі түрі мен математикалық аппарат математикалық үлгілеудің мақсаттары мен міндеттері арқылы анықталады: парктикалық сипатты, қарапайым есептерді шешу күрделі емес тәуелділік, заңдылық түріндегі қарапайым үлгілер көмегімен жүзеге асырылады; іргелі терең сипаттағы күрделі есептерді шешу бірнеше деңгеймен ұсынылатын күрделі үлгілермен сипатталады.

Математикалық үлгілеудің (модельдеудің) түрі зерттелетін үздіксіз үрдіс немесе дискретті үрдіс (процесс) екендігіне де байланысты. Егер үрдіс уақыт бойынша (жол және т.б.) үздіксіз болса, онда ол дифференциалды теңестірумен жеңіл және дұрыс үлгіленеді. Егер зерттеліп отырған нысанда негізгі параметр уақыт және амплитуд бойынша квантталса, автомат теориясын пайдаланған жөн.

Математикалық үлгілеудің үшінші кезеңі нысанның параметрлер шектігін және оның сыртқы ортамен байланысы сызбасын (шығыс және кіріс параметрлерінің ара қатынасы бойынша) анықтауға апаратын, оның таңдалған түріндегі математикалық үлгі түрін анықтау болып табылады.

Нысанның сыртқы ортамен байланысының барлық нақты нұсқалары келесі шартты атауға ие болатын төрт сызбаға бөлінеді.

Тек бір фактордың G бір көрсеткішке R ықпал етуін қарайтын бір өлшем- бір өлшемді сызба (3.1. сурет). Мысалы, ашық борозда бойынша соқаны кедергісінің өзгеру заңдылығы анықталады:

R_n=Gf

Мұнда f- соқаны сүйрелеу кедергісінің коэффициенті.

G R_n=Gf

►►►

G

3.2. сурет. Салмақ күшіне байланысты соқаны ашық бороздада сүйрелеу кедергісі.

3.2. суретте көрсетілгендей сыртқы орталы нақты бір нысанның бір өлшем-бір өлшемді байланыста кіріс ықпалдары шығыс дабылымен тұрақты (нақты жағдайда) коэффициенті арқылы байланысады (мысалда-f). Үрдіс (процес) стационарлы болмаған кезде көрсетілген байланыс әртүрлі функциялармен, көбінесе- полиномен сипатталады.

Бір өлшем- көп өлшемді сызба параметрлердің өзара байланысы (3.3. сурет).

Q_З

λ Q_П

g

W_C

3.3. сурет Ауа сеператорында дән тазалау үрдісі.

Бұл жағдайда нысанға бір фактор ықпал етеді, ал оның әрекеті бірнеше көрсеткіштермен сипатталады. Мысалы, дән қоспаларын ауа сеператорының жұмыс кеңістігіне берудің теңсіздік деңгейі λ қоспалармен шығарылған дән мөлшеріне Q ₃, дәнмен түсетін қоспалар санына Q_п, дәннің жарақаттануына g және сеператордың өнімділігіне Wс әсер етеді.
Байланыс сызбасы бойынша нысан сыртқы ортамен байланыстың бір өлшем- бір өлшемді сызбасы үлгісіне ұқсас сипатталады.

Параметрлер байланысының көп өлшем- бір өлшемді сызбасында нысанға бірнеше факторлар әсер етуі мүмін, мысалы, агрегаттың жұмыс ені В_аг, оның жұмыс жылдамдығы υ _р және ауысымдағы жұмыс уақытының ұзақтығы Т_рем, оның әрекеті бір шығыс көрсеткіштерімен- ауысым өнімділігімен сипатталады.

Bаг W_cv=В_аг·υ_р·Τ_рсм

υ _р

Τ _рсм

3.4. сурет. Жұмыс еніне В_аг, жұмыс жылдамдығына υ _р және ауысымның жұмыс уақытының ұзақтығына Т_рем,байланысты сепкіш агрегаттың ауысымдық өнімділігі.

W см = В_аг ·υ _р Т_рем, (3.2.)

Қолданбалы ғылымда, сонымен қатар, ауылшаруашылық механизациясында өзара байланыстың бұл түрі өте жиі қолданылады және сыртқы әрекеттердің бір маңыздылығындағы стационарлық нақты үрдістің статистикалық жағдайында нысанды жалпы сипаттау келесі үлгімен жүзеге асырылады.

m

y =a∑x_i

i=1

Сыртқы әсерлердің маңыздылығы бірдей еместігінде келесі түрлі жалпы үлгі қолданылады:

m

y = ∑ a _i ·x_i

i=1

Үрдістің стационарлығы еместе, алдыңғы нұсқалардағыдай келесі үлгі қолданылады:

m₁ m₁ m₂ m₂ m₂

y = a_о + ∑ a _i ·x_i + ∑ ∑ a _i ·x_i x_j + ∑ ∑ ∑a _i ·x_i · x_j x_к + ...,

i=1 j=1 i=1 j=1 к

мұндағы а_i- тұрақты коэффициент

m- нысанға сыртқы әсерлері саны

m₁, m₂ -жұпты, үштік және одан жоғары факторлар әсері (m₁ =c_m ²; m₁ =c_m ³ екені белгілі).

Сәйкес болжамдар мен түрлену нәтижесінде үлгі нақтыланған түрде ұсынылады (3.2) және т.б.

Көп өлшем- көп өлшемді сызба бірнеше фактор әсер ететін нысанды қарау кезінде бақыланады, ал оның бұл ықпалға әрекеті бірнеше көрсеткіштермен сипатталады.

В

К₀ R₂

υ_р R₃

G

3.5. сурет. Соқа мен топырақтың өзара байланысы.

Шығыс және кіріс параметрлерінің өзара байланыстарының мұндай сызбасы топырақты соқамен жырту үрдісі кезінде қолданылады. Нысанға бес кіріс параметрелі әсер етеді: жыртылған жер ені, соқаны қамту ені, топырақтың үлесті кедергісі, агрегат қозғалысының жұмыс жылдамдығы және соқа салмағының күші. Шығыс параметрлері болып келесілер табылады: кедергі, ашық бороздада соқаны сүйрету, қопсыту кедергісі және топырақтың өңделген қабатының бұрылысының кедергісі; топырақтың шашылу кедергісі. Оларды келесі қатынаспен ұсынуға болады:

R₁ = G·f; R₂ =K₀·a·B; R₃ =ξ·a·B·υ²

Соқаның топырақпен өзара байланысының жалпы үрдісін үш құрамадан тұратын жалпы үлгімен сипаттауға болады.

R_пл= G·f +K₀·a·B + ξ·a·B·υ²

Үлгіде (3.3) және (3.4) көрсетілгендей көп өлшем- көп өлшемді өзара байланыстар көп мөлшер- бір мөлшерліге жеткізіледі және нысанның жалпы үлгісі (3.3) түрін немесе иек қана түрленгеннен кейін ғана (3.4) қабылдайды.

Динамикалық нысанның математикалық үлгісін құрастыру зерттеуді дифференциальды теңестіруді құрастыру құрастыруға және ары қарай түрлендіруге ауыстырады. Дифференциалды теңестіру класында динамикалық жүйені үлгілеу әдістемесі, ереже бойынша зерттеліп отырған нысанның ортамен өзара байланысының түрі мен күрделілігіне және кіріс параметрлері мен жүйенің шығыс дабылдарын априорлық білімге байланысты болады.

Неғұрлым қарапайым динамикалық нысандар бірінші тәртіпті толық бір тектес емес дифференциалды теңестірулерді құрастыру және ары қарай түрлендіру жолымен жүзеге асырылады.

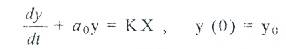
Неғұрлым күрделі жүйелерді сипаттау кезінде дифференциалды екінші тәртіпті теңестіру қолданылады:

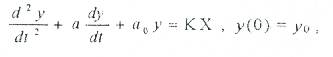
Мұнда, а- дифференциалды теңестіру коэффициенті;

К 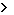0- пропорционалдық коэффициенті;

У₀-шығыс параметрінің бастапқы мағынасы;

Сонымен қатар, кіріс параметрлерінің бір-бірінен тәуелсіздігі жөніндегі болжам олардың нысанға деген әрекеттеріне негізделеді. Бұл жағдайда барлық факторлар сомаға сезгіштік коэффициенттерінің көмегімен келтіріледі (диф теңестірудің оң бөлігінде).

Мұндай болжамға мүмкіншілік болмаса, алдын ала әрбір кіріс параметрлерінің шығыс көрсеткішіне ықпалы белгіленеді және шығыс сипаттардың түрлері бойынша дифференциялды теңестіру түрлері алынады немесе алдыңғыларын тиісті шарттарға сәйкестенгенінше түзетіледі. Сонымен қатар, факторлардың бір уақыттағы әрекеті кезінде шығыс сипаттамасы тәуелсіз дифференциалды теңестірудің әрбір фактор бойынша шешім сомасын ұсынады.

Кіріс және шығыс параметрлері туралы шектеулі мағына кезінде немесе олар толық жоқ болғанда дифференциалды теңестірулер құрылым білімі және зерттеліп отырған нысанның құрылымы негізінде құрастырылады деген болжам бар.

Жоғарыда баяндалғандар негізінде, әмбебап, өмірдің барлық болмысы үшін неғұрлым тұрақты дифференциалды теңестіру құрастыру тәсілі жоқ.

Бірақ та, барлық нақты геометриялық және физикалық есептерді теңестірудің келесі үш түрге әкелумен қортындалатын дифференциалды теңестіруді құрастыру жолында барынша мүмкіндікті ортақтық бар: дифференциалдағы дифференциалды теңестіру; туындыдағы дифференциалды теңестірулер; қарапайым интегральды теңестірулер (ары қарай дифференциалды болып ауысатын). Нақты бір есепті шешу үшін осы үш түрдің (есептің шарттарына неғұрлым сай келетін) бірін таңдау керек, ары қарай оны түрлендіріп, оңтайлы параметрлерді немесе зерттеліп отырған нысанның жұмыс істеу режимін анықтауға ыңғайлы түрге келтіру қажет.