Эксперимент міндетін қалыптастыру

Өткен тарауларда көрсетілгендей, эксперимент алдында үш түрлі міндет қойылуы мүмкін:

- біріздендіру міндеті, яғни, экспериментті тексеру және теориялық зерттеу нәтижелерін нақтылау міндеті;

- теориялық зерттеу нәтижелерін толықтыру міндеті;

- оңтайландыру міндеті, яғни, алдыңғы теориялық зерттеусіз өзіндік дербес экспериментті зерттеу міндеті.

Міндет типінің былай бөлінуі нақты зерттеудегі нақты міндетті қалыптасуын анықтайды.

Нақты міндетті дұрыс қалыптастыру міндетті шешуден гөрі маңызды орын алып жататын кездері жиі болады.

Эксперимент міндетін нақты қалыптастыру үшін қалыптасқан жағдайды ғана емес, оны шешудің болжалды тәсілдері мен құралдарын да білу керек. қалыптасқан жағдай не алынған теориялық мәннің кемшілігінде, не түзету деңгейінде немесе оның мүлдем жоқтығында болуы мүмкін.

Көптеген классикалық зерттеулерде эксперимент ғылыми жұмыс гипотезасы қалыптастырылғаннан кейін немесе зерттелетін үдеріс, құбылыстың математикалық үлгісін теориялық зерттеу нәтижесінде әзірленгеннен кейін жүргізіледі.

Эксперимент міндеті мен оның қалыптасуы көбінесе теориялық зерттеу нәтижелеріне байланысты болады. Теориялық білім, әдетте, зерттеуші алдына қойылған мәселені не міндетті толық шеше бермейді. Теориялық зерттеуді талдау кезінде міндеттің шешілмеген элементтері анықталады, осылар эксперимент міндетінің негізін құрайды.

Біріздендіру міндетін қалыптастыру теориялық тұрғыдан зерттелген нысан параметрлерін нақты анықтаудан тұрады, ол нысан параметрлерінің дұрыстығын эксперименталды зерттеумен тексеру керек. Басқаша айтқанда, міндет теориялық зерттеу нәтижелерін тексеріп, нақтылаудан тұрады.

Теориялық тұрғыдан дәл сипаттау қиындық туғызатын немесе мүлдем мүмкін болмайтын құбылыстар, үдерістер де болады. Бұндай жағдайда теориялық зерттеу нәтижесінде математикалық үлгілеуге коэффициенттер, мәндер енгізіледі, ал оларды эксперменталды түрде (ғылымның осы саласының даму деңгейіне байланысты) ғана анықтауға болады. Мұндай математикалық үлгінің практикалық шешімі осы параметрлер мен коэффицииенттер мәнінің белгісіздігі салдарынан қиын.

Мұндай типті эксперименттің міндетін қалыптастыру осы математикалық үлгіге кіретін параметрлер мен коэффициенттерді анықтаудан байқалады.

Міндет қалыптастырылғаннан кейін экспериментті жоспарлау жүзеге асырылады.

Мысалы, топырақ қорғау топырақ өңдеу машиналарын жетілдірудің тиімді бағытын анықту мақсатында желдің топырақ бөліктерімен өзара күшті әсерінің математикалық үлгісі құрылады:

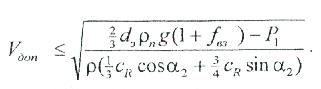
Үлгі топырақтың желдік эрозиясы орын алмайтын шекті шартты сипаттайды. Осы үлгіні жел жылдамдығына Vқос және топырақ бөлігінің диаметріне dэ қатысты шешіп, топырақ жел эрозиясына ұшырамайтын, яғни, dэ бөлігі желмен ұшып, орын ауыстырмайтын сыни мәнді анықтауға болады. Алайда, төмендегі параметрлер мәні белгісіз болғандықтан, бұл үлгіні шешу іс жүзінде мүмкін емес:

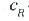– толық аэродинамикалық күш коэффициенті;

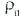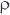және – топырақ пен ауаның сәйкес тығыздығы;

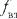– топырақ бөліктерінің байланыс коэффициенті.

Бұл параметрлер мен коэффициенттерді тек экспермент жолымен ғана анықтауға болады. Эксперимент типті міндетті қалыптастырудың мәні де осында. Көптеген инженерлік зерттеулер міндеттің осы екі типіне жатады.

Алайда, техникалық ғылым саласында ғылым дамуының осы деңгейінде теориялық тұрғыдан шешу мүмкін болмайтын мәселелер де бар. Бұл жағдайда ғылыми жұмыс гипотезасы ұсынылады (әзірленеді), соған бейімделіп, оңтайландыру міндеті, мәселені эксперимент жолымен шешудің ең тиімді әдісін іздеу міндеті қалыптасады. Мұндай оңтайланған жоспар бойынша орындалған эксперимент типі болжалды теориялық зерттеусіз жүргізілетіндіктен, олардың нәтижелері жеткілікті, ал дұрыстың деңгейі жоғары болып есептеледі де, оларды балама тексеру талап етілмейді.

Эксперименттік зерттеу мәселелері мен міндеттерін қалыптастыру кезінде мақсатты функция мен тәуелсіз ауыспалыларды анықтау өте маңызды:

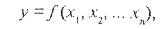
мұндағы: у – мақсат функциясы;

х₁ – зерттеу нысаны қызмет ететін тәуелсіз ауыспалылар (факторлар).

Егер эксперименттің оңтайландыру міндеті болса, онда мақсатты функция белгісіз регрессия коэффициенттерімен жарты номиналды теңдеу түрінде берілуі мүмкін:

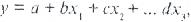
Мұндағы: a, b, c, d – регрессия коэффициенттері

Мысалы, у мақсат функциясы ретінде топырақ өңдейтін машинаның жұмыс органына топырақтың шекті кедергісін таңдауға болады, тәуелсіз ауыспалылар (факторлар) ретінде х1 топырақтың тығыздығы, х2 механикалық құрамы және хэ ылғалдылығы алынады.

Фактор кезінде регрессия коэфициентімен жарты номиналды теңдеу зертеу үдерісінің қызметін сипаттайды, отклик беті атанған геометриялық бет түрінде ұсынылады.