Теориялық зерттеуді талдау және бағалау

Жоғарыда баяндалғандарды талдай отырып, дифференциалды теңдеу құбылыстардың, үдерістердің тұтас класының, тұтас жиынтығының үлгісінен тұратыны туралы қорытынды жасауға болады. Оларды талдау және жекелей интеграциялау бастапқы дифференциалды теңдеуді қанағаттандыратын көп шешімді береді. Зерттеушінің алдына нақты тапсырма қойылады. Сондықтан да көптеген болжалды шешімдер арасынан қарастырылып отырған үдерісті (зерттеу нысанын) ғана қанағаттандыратын бір шешімді алу үшін қосымша жағдай жасалады. Сөйтіп, зерттеу үдерісі өзі жататын тұтас кластан нақты ажыратылған болуы керек.

Таңдалған теңдеудің барлық ерекшеліктерін ашатын барлық шарттар бірмәнді шарттар деп аталады. Бірмәнділік шарты келесі қасиеттермен, белгілермен: нысанның геометриялық параметрлерімен (жұмыс органының негізгі параметрлерімен, мәселен, сынаны еріту бұрышы, түренді орнату бұрышы, қармауыш ені т.б.); зерттеу нысанының физикалық қасиетімен (топырақтың ылғалдылығы, тығыздығы, тұтқырлығы, беріктігі және т.б.); зерттеу нысанының бастапқы сәттегі жағдайын сипаттайтын бастапқы шарттармен (сепкіш түренінің табан асты кеңістігінде таратқыш траекториясын зерттеу кезінде тұқымның таратқыштан түсу қозғалысының жылдамдығы, қалқан астындағы қардың жатуын зерттеу кезінде қалқан алдындағы қар-ауа ағынының жылдамдығы); қоршаған ортамен шекарада зерттелетін жүйелердің өзара әсері шегімен сипатталатын шекаралық шарттарымен (мысалы, түрен жүйесінің параметрлерін оңтайландыру кезінде шекті шарт болып олардың ұзындық бойындағы шекті өлшемі табылады, ол өлшемдер раманың сепкішті өндіруші зауыт конвейердің конструкторымен анықталатын базалық өлшемінен аспауы керек) сипатталады. Зерттеу нысанының қызметінің негізгі параметрлері мен режимдерін негіздеу үдерісінде бастапқы және шекті шарттар оңтайландырудың жиекті шаттары деп аталады.

Мысал ретінде қарапайымдылығына қарамай, ғылыми зерттеудің дифференциалды теңдеу класындағы математикалық аппаратты қолданумен жоғарыда аталған барлық элементтері қамтылатын оңай зерттеу жұмысы жүргізіледі.

Зерттеу топырақ ылғалдылығы аз және топырақтың жел эрозиясына ұшыраған жағдайында астық дақылдарын топырақ астына шашыратып себуге арналған сепкіш жасаумен байланысты.

Сонымен, астық тұқымын қоректендіргіш алаңына теңдей таратып, топырақ астына тереңдей себу арқылы астық дақылдарының өнімділігін арттыру мәселесі бар.

Осы мәселені шешу кезінде қарама-қайшы позиция түрінде мәселелі жағдай қалыптасты.

Қазіргі қатарлап себудің негізгі кемшіліктерінің бірі тұқымның қатарға шоғырланып, қатар аралығына түспеуінде (бір жерде қалың, бір жерде дым да жоқ), осыған орай, тұқым тегіс себілмейді де, қоректендіру алаңы (егіс даласын) өсімдікпен толық пайдаланылмайды.

Сәйкесінше, тұқымды қоректендіру алаңына тегіс шашу үшін олардың қатардағы аралығын ұлғайтып, қатар арасындағы аралығын азайту керек. Ал ол үшін қатарды қалыптастыратын түрен дискілері арасындағы қашықтықты азайту керек, бұл дискілердің топырақпен және ондағы өсімдік қалдығымен толып қалмау шартына қайшы келеді. Бұл қарама-қайшы жағдайдан қажетті балама теориясы арқылы, яғни, топырақта тұқымды тегіс таратуға және топырақпен толып қалмауға мүмкіндік беретін механика құралын жасап шығару арқылы құтылуға болады.

Аталған мәселені культиватор табаны түріндегі жұмыс органын қолдану жолымен іске асыруға болады, сөйтіп, табан асты кеңістігіне қармауыш ені бойымен тұқымды тегіс таратуға болады деген гипотеза ұсынылды.

Жоспарда 1, 2, 3 ...n қарапайым сектор түріндегі табан асты кеңістікті, ал 1,2,3...n қарапайым жолақ түріндегі қармауыш енін қарастырып, егер әр жолақ бойындағы тұқым саны бірдей болса, тұқымның таратылуын қанағаттанарлық деп есептеуге болады (сурет 3.6).

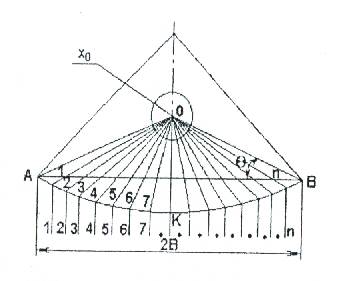
Сурет 3.6 – Жоспардағы жұмыс органының сызбасы

Егер төмендегі шарт орындалса, бұл мүмкін болады:

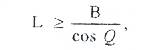
Мұндағы: L – тұқымның таратқыштан ұшу ұзақтығы;

Q – тұқым ұшу жазықтығының шекті бұрышы;

2В – түреннің толық қалмауын қамтамасыз ететін қармауыш ені.

Астықты материалды нүкте ретінде қабылдап және ауа кедергісін ескеріп (... бұл кездегі жіберілер қателік 0,6...0,7 %) қозғалыстың дифференциалды теңдеуін төмендегідей жазады:

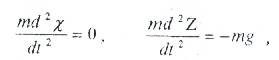
Мұндағы: m – астық салмағы.

Осы теңдеуді екі рет бастапқы қозғалыс шартымен интеграциялағаннан кейін теңдеуден t параметрін алып тастап, астықтың таратқыш бетіне шыққаннан кейінгі қозғалыс траекториясының теңдеуін аламыз:

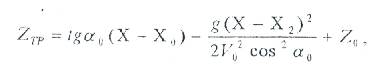
Мұндағы: V₀ – таратқыштан шыққаннан кейінгі астық қозғалысының бастапқы жылдамдығы;

А ₀ – бастапқы жылдамдық бағытының бұрышы;

Z₀ – таратқыш қондырғысының биіктігі;

X₀ – таратқыш негізінің радиусы.

(3.9) алынған мән тұқымды таратудың жалпы түрдегі үлгісін береді.

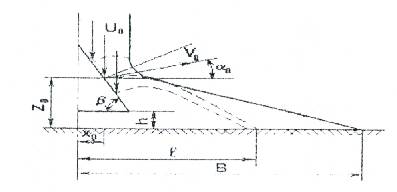
Сурет 3.7 – топырақ ішіне шашыратқыш түреннің көлденең-тік жазықтықтағы жұмысы сызбасы

Бұл таратқыштың негізгі параметрлерін одан әрі талдап, негіздеуге мүмкіндік береді. Алдында қойылған міндет пәніне қарапайым талдау жасайық. (3.9) үлгісі астықтың ұшу траекториясын сипаттайды. Бұл траектория параметрлері (Z) түрлі мәнді иеленуі мүмкін, алайда бізге бойымен қозғалу арқылы астықтың табан асты кеңістігінің күмбезіне соғылмауын болдырмайтын траектория керек. Ең ұзақ ұшуды күмбезді астық күшінің импульсісіз жанасатын траектория қамтамасыз етеді. Тек осы жағдайда ғана ұшу ұзақтығы берілген мәнді иеленеді.

Тұқымның ұшу траекториясы мен жыртылған жер түбінің қиылысу нүктесінің абсциссасы олардың ұшу ұзақтығын көрсетеді, ол (3.9) формуласымен Z=0 (жыртылған жер деңгейінде Z=0) көрсеткішін қабылдап, анықталады:

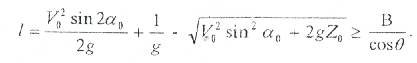
(3.10) формуласы есебімен тұқымның ұшу қашықтығын қанағаттандыру шарты былай жазылады:

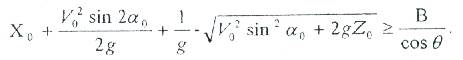(3.11).

Осыған орай, тік жазықтықта ұшып, таратқыштың 0 орталығы мен түрен табанының ұштығының соңы арқылы өтетін тұқым ең қолайсыз жағдайда болады, себебі осы жазықтық қимасы жыртылған жер түбіне көлбеу бұрышының ең аз көрсеткішіне ие, бұл осы жерде ең төмен күмбез болатынын көрсетеді.

Сәйкесінше, астықтың күмбезге соғылмай түрен кеңістігінде ұшуы, осыған орай, тұқымды қоректендіру алаңы бойынша тең таралуы мына жағдайда орын алады:

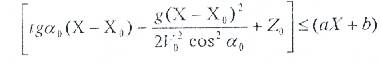(3.12)

Мұндағы: Z=ax+b – кеңістіктегі күмбездің астық ұшуы үшін ең нашар жағдайының теңдеуі.

Дифференциалды теңдеу формасындағы математикалық аппарат көмегімен нысанның математикалық үлгісін қалыптастырудың барынша мұқият қарастырылған мысалы және оның талдамасы зерттеудің мұндай әдісінің артықшылығын және зерттеушіні нақты қызықтырған параметрлерді негіздеу пәніне талдау жасау мүмкіндігін көрсетеді.