Длина пути. Вектор перемещения
В физике используются различные модели: при описании объектов выделяются их главные качества и отбрасываются второстепенные (материальная точка, абсолютно твердое тело, абсолютно упругий и неупругий удары, идеальный газ, черное тело, линейный осциллятор и т.д.).
Построение физико-математической модели, как правило, выполняется методом последовательных приближений. В первом или нулевом, самом грубом, приближении учитывают только самые необходимые аспекты (свойства) процесса (тела), математические уравнения при этом обычно самые простые и легко разрешимы аналитически. Проведя расчет по этим уравнениям, результат сравнивают с данными эксперимента. При удовлетворительном согласии данных останавливаются на полученной модели (описании) процесса (тела). При несогласии (второе и т.д. приближение) вносят в рассмотрение новые факторы, усложняются описывающие явление уравнения, они уже могут не решаться в явном виде (аналитически), а только численно, процесс повторяется до получения с требуемой (необходимой) точностью согласия теоретических и достаточно большого числа экспериментальных данных.
Примеры физико-математических моделей:
- материальная точка – это тело, размеры которого в данной задаче несущественны;
- абсолютно твердое тело – тело, которое ни при каких условиях не деформируется, при этом расстояние между любыми двумя точками тела остается неизменным.
Механика изучает механическое движение. Механическое движение – это взаимные изменения положения тел друг относительно друга или взаимного расположения частей тела. Любому описанию механического движения тела должен предшествовать выбор системы отсчета (СО). Она состоит из какого-либо неподвижного твердого тела (отсчета) и связанной с ним системы координат, в которой указывается начало отсчета времени. В механике чаще всего используется координатная форма описания движения: положение материальной точки задается ее радиус-вектором 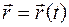 . Это уравнение эквивалентно трем скалярным: x=x(t); y=y(t); z=z(t).
. Это уравнение эквивалентно трем скалярным: x=x(t); y=y(t); z=z(t).
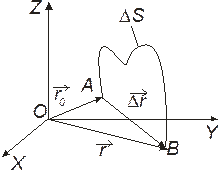
Рис. 1.1
Рассмотрим (рис. 1.1) движение материальной точки вдоль произвольной траектории. Отсчет времени начинают с момента, соответствующего точке А. Длина участка АB, пройденного телом с начала отсчета времени, называется длиной пути Δs и является скалярной функцией времени.
Вектор 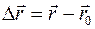 называется перемещением тела. В случае прямолинейного движения
называется перемещением тела. В случае прямолинейного движения 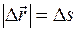 . Сказанное справедливо для движения в одном направлении, а в общем случае
. Сказанное справедливо для движения в одном направлении, а в общем случае 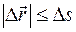 .
.
Траектория– это линия, которую описывает тело при движении в пространстве. Если траектория лежит в одной плоскости, движение называется плоским или двумерным (движение тела, брошенного под углом к горизонту, движение заряженной частицы в магнитном поле, когда скорость перпендикулярна вектору магнитной индукции 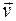 ^
^ 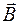 .
.
Дата добавления: 2015-05-05; просмотров: 1269;
