Скорость. Ускорение.
Для характеристики движения тела вводится векторная величина – скорость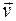 
, которая определяет быстроту движения и его направление в данный момент времени t.
Если тело проходит за время Δt путь Δs, модуль которого равен Δr (при условии малости промежутка Δt), скорость определяется как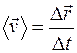 
- средняя скорость(м/c); 
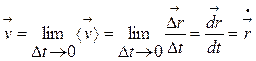– мгновенная скорость (всегда направлена по касательной в данной точке траектории).
Тогда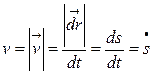 
и 
.
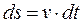Следовательно,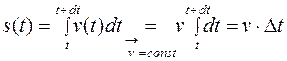 
.
Движение, при котором скорость постоянна, называется равномерным. В случае неравномерного движения важно знать, как изменяется скорость с течением времени, по модулю (величине)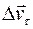 
и направлению 
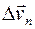(последний интеграл будет иметь другой вид). Для этого вводят векторную величину – ускорение 
.
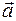Среднее ускорение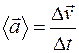 
(м/c2), а мгновенное 
.
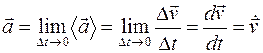Как и скорость, ускорение можно в любой момент времени представить в виде двух составляющих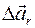 
(
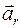– тангенциальной) и 
( 
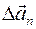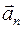– нормальной): по теореме Пифагора (ок. 580–500 гг. до н.э.) 
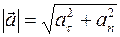, так как ^ ,
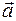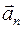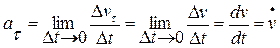. (1.1)
Нормальная составляющая:
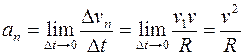, (1.2)
где R – радиус кривизны траектории в данной точке.
В зависимости от значени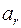й 
и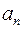 
, можно выделить следующие типы движения:
1. 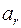=0, =0 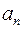– равномерное движение;
2. 
, 
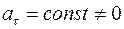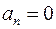– равнопеременное прямолинейное движение; при этом 
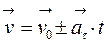(1.3), тогда
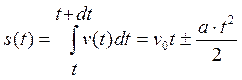. (1.4)
Следует помнить о различии в общем случае изменения пути и координат(ы): не всегда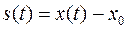 
.
3. 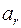=0, 
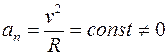– равномерное вращение по окружности, так как R=const. В общем случае 
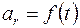и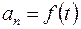 
.
Дата добавления: 2015-05-05; просмотров: 1032;