Кинематика вращательного движения. При описании вращательного движения пользуются осевыми или аксиальными (axse – лат., axis – англ.)векторами (псевдовекторами)
При описании вращательного движения пользуются осевыми или аксиальными (axse – лат., axis – англ.)векторами (псевдовекторами). Направление их связано с поступательным движением винта, закручиваемого слева направо вращением тела по окружности (правого винта). Эти скользящие вектора не имеют строго определенной точки приложения, в отличие от полярных векторов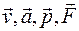 
, и могут быть отложены из любой точки на оси вращения (рис. 1.3): 
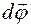(характеризующий угол поворота), 
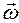и 
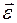(угловые скорость и ускорение).
Можно провести сопоставление угловых (при вращательном -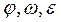 
) и линейных (при поступательном движении – 
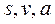) величин.
Так,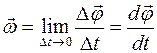 
(рад/с), а 
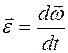(рад/с2) – при равноускоренном вращении вектора 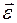сонаправлен с вектором 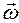, а при равнозамедленном – противонаправлен.
С учетом равенства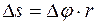 
имеют:
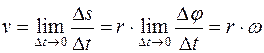или векторно 
.
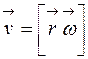Рис. 1.3
Согласно формулам (1.1) и (1.2), получают:
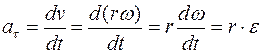
и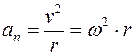 
.
При вращении тела относительно неподвижного начала (точки, оси) все его точки движутся с равными угловыми скоростями
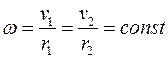, но с различными линейными.
При равномерном вращении его характеризуют периодом T и частотой n вращения. Период – время поворота на угол 2p: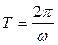 
, а частота – число полных оборотов в единицу времени: 
.
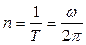Аналогично (см. формулы (1.3) и (1.4), сопоставляя s-j, w-v, e-ar) можно получить для равнопеременного вращения по окружности зависимости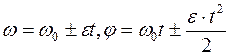 
.
Дата добавления: 2015-05-05; просмотров: 839;