Б) Изображения синусоидальных величин в векторной форме

Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.

Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω.

Проекция отрезка на вертикальную ось в начальный момент времени .

Когда отрезок повернется на угол α₁, проекция его .

Откладывая углы α₁, α₂, ...

на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 35.2).

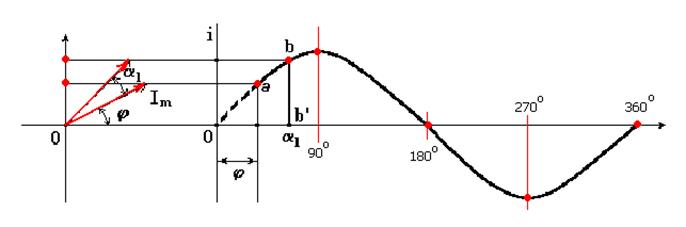
Рис.35.2. Представление синусоидальной величины в векторной форме

Пусть даны два синусоидальных тока:

.

Нужно сложить эти токи и получить результирующий ток:

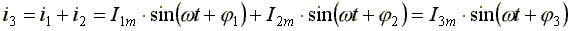
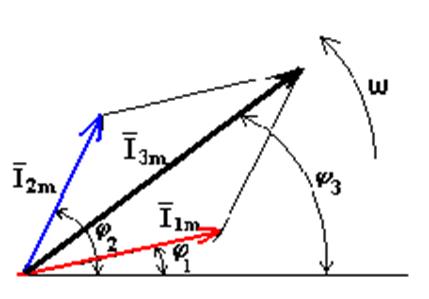
Рис.35.3.Сложение векторов двух величин

Представим синусоидальные токи i₁ и i₂ в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ₁ и φ₂ относительно горизонтальной оси.

Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 35.3).