Уравнение неразрывности

Выделим в движущемся газе элементарный объем в форме параллелепипеда (рис. 8.2) и запишем условие неизменяемости массы во времени для этого элемента. Это условие будет выражать закон сохранения массы:

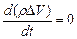, (8.12)

где 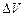- объем элемента;

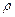- средняя плотность элемента.

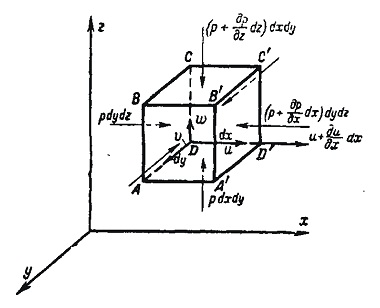
Рисунок 8.2 Схема течения потока через стенки элементарного параллелепипеда

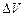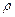Дифференцируем, имея в виду, что и - переменные величины:

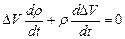. (8.13)

Разделив уравнение (8.13) на 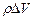, получим уравнение неразрывности в виде:

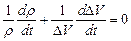. (8.14)

Производная 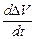выражает скорость изменения объема или, следовательно, скорость объемной деформации жидкой частицы, а 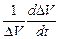представляет собой скорость относительной объемной деформации.

Определим величину скорости относительной объемной деформации частицы, выразив ее через соответствующие проекции скорост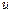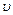и , и 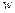. Подсчитаем линейную деформацию частицы в направлении оси 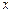(рис. 8.2). Скорость левой грани ( 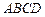) равна 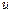, а скорость правой ( ) - .

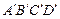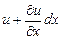Предположим, что в пределах каждой из рассматриваемых граней параллелепипеда скорости постоянны. За элемент времени 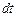левая грань 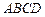переместится на расстояние 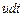вправо. За тот же отрезок времени грань 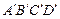переместится в том же направлении на расстояние 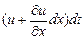. Следовательно, объем элемента изменится, так как скорости этих двух граней различны. Подсчитав абсолютное изменение объема частицы по направлению оси 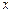, получим:

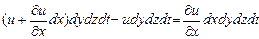. (8.15)

Рассуждая аналогично, для других двух пар граней можно получить приращения объема частицы по осям 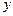и 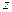в следующем виде:

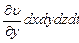, (8.16)

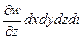. (8.17)

Полное изменение объема частицы определяется как сумма этих приращений.

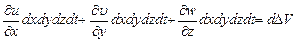
Следовательно, скорость относительной объемной деформации определяется:

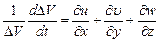, (8.18)

так как объем элемента .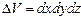

Подставив (8.18) в уравнение неразрывности (8.14), получим:

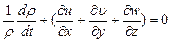. (8.19)

Частные производные 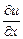, , 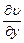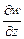определяют величины скоростей относительных линейных деформаций граней параллелепипеда.

Так как 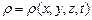, то полная производная плотности равна:

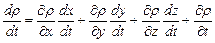. (8.20)

Имея в виду, что 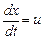, , 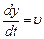, 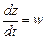получим:

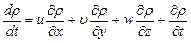. (8.21)

Представим уравнение (8.19) в следующем виде:

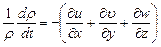
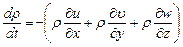
и учитывая (8.21) получим:

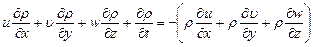
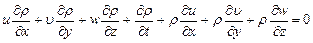
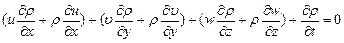
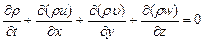. (8.22)

Если движение является установившимся, то .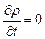

Уравнение (8.22) является уравнением неразрывности газового потока в дифференциальной форме. Это уравнение было впервые получено Эйлером в 1659 г.