Движение жидкой частицы
В общем случае движение жидкой частицы является сложным. Наряду с поступательным движением вдоль некоторой траектории частица может вращаться относительно собственных осей и в процессе этого движения деформироваться.
Благодаря неодинаковым скоростям на различных гранях частица испытывает линейную деформацию и деформацию скашивания или сдвига. Если в первоначальный момент движения частица имела форму параллелепипеда, то с течением времени вследствие деформации форма ее изменяется. В случае сжимаемой жидкости меняется также и объем частицы.
Рассмотрим вращение и деформацию одной из граней параллелепипеда (рис. 8.1).
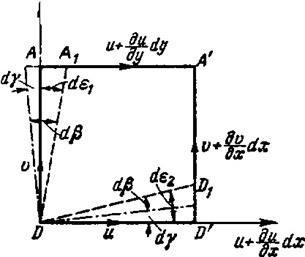
Рисунок 8.1 – Движение жидкой частицы
Перемещения ребер 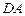 и
и 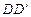 вызваны как вращением плоского жидкого элемента (грани параллелепипеда), так и его деформацией. Если бы грань только деформировалась, без вращения, то ребра
вызваны как вращением плоского жидкого элемента (грани параллелепипеда), так и его деформацией. Если бы грань только деформировалась, без вращения, то ребра 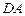 и
и 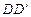 поворачивались бы на одинаковый угол навстречу друг другу или в противоположных направлениях. Наоборот, если бы грань совершила только вращательное движение (как абсолютно твердое тело), то ребра
поворачивались бы на одинаковый угол навстречу друг другу или в противоположных направлениях. Наоборот, если бы грань совершила только вращательное движение (как абсолютно твердое тело), то ребра 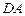 и
и 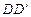 поворачивались бы на одинаковый угол в одном направлении.
поворачивались бы на одинаковый угол в одном направлении.
Движение элемента в общем случае можно рассматривать как сумму деформационного и вращательного движений и таким путем определить углы 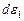 и
и 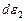 . Принимая, что в результате вращения (против часовой стрелки) ребра
. Принимая, что в результате вращения (против часовой стрелки) ребра 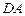 и
и 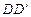 повернулись на угол
повернулись на угол 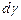 , а в результате деформации - дополнительно на угол
, а в результате деформации - дополнительно на угол 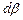 , найдем:
, найдем:
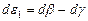 и
и 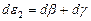 , (8.6)
, (8.6)
где 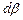 и
и 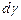 - углы, соответственно деформационного и вращательного движения частиц.
- углы, соответственно деформационного и вращательного движения частиц.
Из уравнений (8.6) получим:
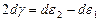 . (8.7)
. (8.7)
Угловая скорость вращения грани будет равна:
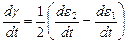 . (8.8)
. (8.8)
Так как 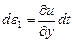 и
и 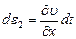 (рис. 8.1), то выражение (8.8) принимает следующий вид:
(рис. 8.1), то выражение (8.8) принимает следующий вид:
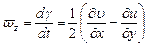 , (8.9)
, (8.9)
где 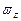 - составляющая вектора угловой скорости вращения, параллельная оси
- составляющая вектора угловой скорости вращения, параллельная оси 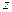 (индекс
(индекс 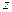 указывает направление оси, относительно которой происходит вращение).
указывает направление оси, относительно которой происходит вращение).
По аналогии получаем, что угловые скорости вращения двух других граней, расположенных в плоскостях 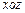 и
и 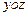 , выражаются через соответствующие значения частных производных, причем вращение каждой грани параллелепипеда определено двумя угловыми скоростями:
, выражаются через соответствующие значения частных производных, причем вращение каждой грани параллелепипеда определено двумя угловыми скоростями:
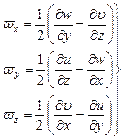 , (8.10)
, (8.10)
Уравнения (8.10) выражают компоненты вектора угловой скорости вращения жидкой частицы 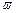 , величина которого определяется как геометрическая сумма:
, величина которого определяется как геометрическая сумма:
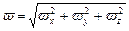 . (8.11)
. (8.11)
Формулы (8.10) определяют в дифференциальной форме связь между составляющими угловой скорости вращения и составляющими скорости поступательного движения.
Вращательное движение частицы вокруг осей, проходящих через частицу, называют вихревым движением. Опыт показывает, что во всех случаях движения реальной (вязкой) жидкости все поле потока или часть его являются вихревыми. В тех областях течения, где вихревое движение частиц отсутствует, угловая скорость вращения равна нулю ( 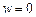 ). В этих областях частицы жидкости могут двигаться по траекториям любой формы, деформируясь при этом, но не вращаясь относительно своих осей.
). В этих областях частицы жидкости могут двигаться по траекториям любой формы, деформируясь при этом, но не вращаясь относительно своих осей.
Если в частном случае при 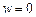 траектории частиц являются замкнутыми кривыми, то такое движение будет частным случаем циркуляционного движения. Следует подчеркнуть, что при таком движении частицы совершают вращение вокруг некоторой оси, расположенной вне траектории, но не вращаются относительно собственных осей.
траектории частиц являются замкнутыми кривыми, то такое движение будет частным случаем циркуляционного движения. Следует подчеркнуть, что при таком движении частицы совершают вращение вокруг некоторой оси, расположенной вне траектории, но не вращаются относительно собственных осей.
Дата добавления: 2015-04-29; просмотров: 1645;
