Уравнения количества движения

Рассматривается движение газа без внутреннего теплообмена при отсутствии теплопроводности и трения. Такое движение является идеализированной моделью действительного движения, в котором проявляются силы трения, возникают градиенты температуры и совершается внутренний теплообмен между соседними частицами.

Выделим в потоке жидкости элементарный параллелепипед. Внутри замкнутой поверхности параллелепипеда заключена масса жидкости. Изменение количества движения массы газа, сосредоточенной внутри поверхности, происходит в общем случае вследствие того, что каждая частица, перемещаясь, занимает с течением времени новое положение и приобретает новую скорость, а также потому, что в каждой точке пространства скорость изменяется во времени. При установившемся движении количество движения меняется только в связи с изменением положения частиц.

Теорема количества движения: «Изменение количества движения массы, заключенной в выделенном элементе, равно импульсу внешних сил». Составим уравнения импульсов в проекциях на координатные оси (рис. 8.2).

Импульс силы - это векторная физическая величина, равная произведению силы на время её действия.

За конечный промежуток времени эта величина равна определенному интегралу элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.

На грань 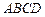в направлении оси 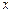: действует сила давления 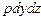, импульс которой будет - .

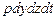Импульс сил давления, действующих на грань 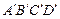, равен: .

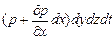Кроме сил давления, на элемент могут действовать массовые силы (гравитационные, магнитные и электростатические). Из них чаще всего необходимо учитывать гравитационную силу - силу тяжести.

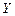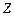Обозначим через , , и проекции единичной массовой силы (отнесенной к массе жидкости) на оси координат 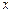, 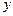и 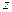. Тогда проекции полной массовой силы на координатные оси будут:

, , .

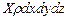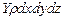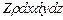Импульс массовых сил в проекции на ось 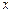будет равен .

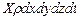И́мпульс (количество движения) - векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы 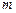этой точки на её скорость 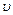, направление импульса совпадает с направлением вектора скорости:

.

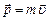Тогда суммарный импульс равен изменению количества движения:

,

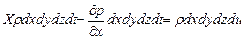где 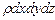- масса элемента.

Откуда получаем:

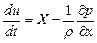. (8.23)

Аналогичные уравнения получаем в проекции на ос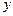и и :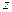

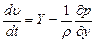; (8.24)

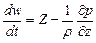. (8.25)

Имея в виду, что приращения скорости равны:

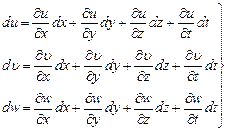(8.26)

подставив (8.23), (8.24) и (8.25) в (8.26) получим систему уравнений для проекций ускорения на координатные оси:

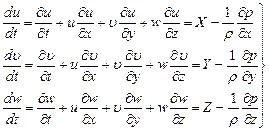(8.27)

Производные 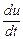, 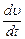и 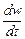выражают проекции полного ускорения движущейся частицы. Уравнения (8.27) показывают, что ускорение жидкого элемента вызывается соответствующими изменениями сил давления, действующих на этот элемент, и массовыми силами. Уравнения (8.27) были также получены Эйлером.