Кинематика материальной точки при криволинейном движении.

Криволинейное движение – движение, при котором траектория – кривая линия. Если материальная точка движется по произвольной кривой, то эту кривую надо разбить на малые дуги и каждую из них совместить с дугой некоторой окружности. Каждая такая окружность называется окружностью кривизны, а радиус называется радиусом кривизны траектории в данной точке.

Рассмотрим один из видов криволинейного движения – движение материальной точки по окружности.

1 случай: равномерное движение по окружности, когда скорость по величине является постоянной | 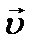|=const, но изменяется по направлению (см. рис.4.2). Изменение скорости по направлению характеризует нормальное (центростремительное) ускорение: .

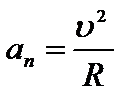Вектор нормального ускорения направлен по радиусу к центру окружности.

2 случай. Скорость движущейся по окружности материальной точки изменяется по величине и направлению: 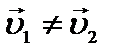. В этом случае ускорение определяется из соотношения: Þ .

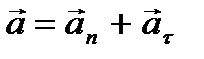Первое слагаемое является нормальным ускорением, второе 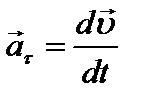– тангенциальное ускорение, направленное по касательной к траектории. 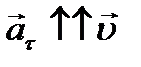– если движение ускоренное; 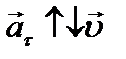– если движение замедленное.

Таким образом, при криволинейном движении полное ускорение состоит из двух составляющих: нормальное ускорение 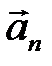– характеризуется изменением скорости по направлению; тангенциальное ускорение 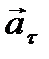характеризуется изменением скорости по величине.