Связь между линейными и угловыми величинами.

Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Пусть твердое тело вращается вокруг неподвижной оси ОО’. Рассмотрим бесконечно поворот тела вокруг этой оси. Угол поворота будем характеризовать вектором 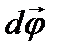 , модуль которого равен углу поворота, а направление совпадает с осью ОО’ так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора
, модуль которого равен углу поворота, а направление совпадает с осью ОО’ так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора 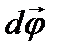 .
.
Найдем перемещение точи А. Положение точки А зададим радиусом-вектором 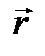 , проведенным из некоторой точки О на оси вращения. Линейное перемещение конца радиуса-вектора связано с углом поворота
, проведенным из некоторой точки О на оси вращения. Линейное перемещение конца радиуса-вектора связано с углом поворота 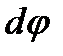 соотношением:
соотношением: 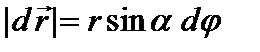 или в векторном виде:
или в векторном виде: 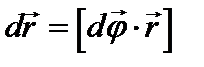
Равенство справедливо для бесконечно малого поворота 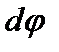 .
.
Векторы, направление которых связывают с направлением вращения, называют аксиальными. Вектор 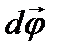 является аксиальным.
является аксиальным.
Введем векторы угловой скорости и углового ускорения.
Вектор угловой скорости 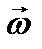 определяют как:
определяют как: 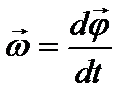 . Вектор
. Вектор 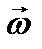 совпадает по направлению с вектором
совпадает по направлению с вектором 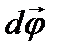 и представляет собой аксиальный вектор.
и представляет собой аксиальный вектор.
Изменение вектора 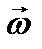 со временем характеризуется вектором углового ускорения
со временем характеризуется вектором углового ускорения 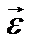 , который определяют как
, который определяют как 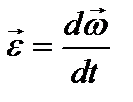 . Направление вектора
. Направление вектора 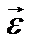 совпадает с направлением
совпадает с направлением 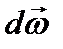 – приращением вектора
– приращением вектора 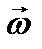 . Вектор
. Вектор 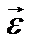 также является аксиальным.
также является аксиальным.
При равномерном вращении 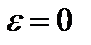 и
и 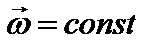 .
. 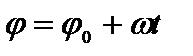 , где jо– начальное угловое перемещение.
, где jо– начальное угловое перемещение.
Вращательное движение характеризуется периодом Т и частотой вращения n.
Частота вращения 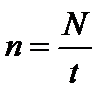 , или
, или 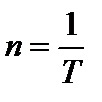 , где N – число оборотов, совершаемых телом за время t; T - период вращения (время одного полного оборота).
, где N – число оборотов, совершаемых телом за время t; T - период вращения (время одного полного оборота).
Для угловых перемещения и скорости: 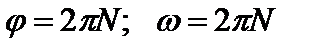 .
.
При равнопеременном (e=соnst) вращении 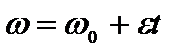 ,
,
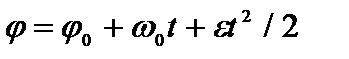 , где
, где 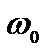 – начальная угловая скорость.
– начальная угловая скорость.
Установим связь между линейными и угловыми величинами.
Найдем скорость 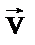 произвольной точки А твердого тела, которое вращается вокруг оси с угловой скоростью
произвольной точки А твердого тела, которое вращается вокруг оси с угловой скоростью 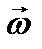 . Формулу
. Формулу 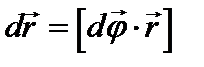 поделим на соответствующий промежуток dt:
поделим на соответствующий промежуток dt: 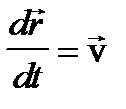 и
и 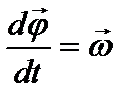 ,
,
тогда 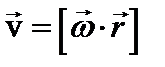 (*).
(*).
Т.е. скорость 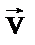 любой точки А твердого тела, вращающегося с угловой скоростью
любой точки А твердого тела, вращающегося с угловой скоростью 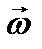 , равна векторному произведению
, равна векторному произведению 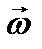 на радиус-вектор
на радиус-вектор 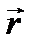 точки А относительно произвольной точки О оси вращения.
точки А относительно произвольной точки О оси вращения.
Модуль вектора скорости 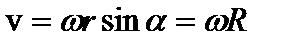 , где R–радиус окружности, по которой движется точка А. Таким образом,
, где R–радиус окружности, по которой движется точка А. Таким образом, 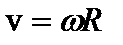 .
.
Продифференцируем (*) по времени: 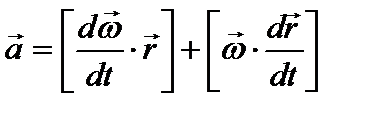 .
.
Так как 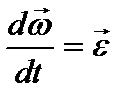 ,
, 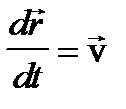 =
= 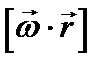 , то
, то 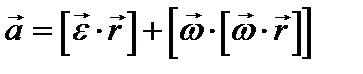 .
.
Здесь вектор 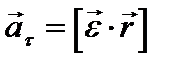 – тангенциальное ускорение, а вектор
– тангенциальное ускорение, а вектор 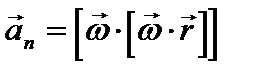 – нормальное ускорение. Модули этих ускорений:
– нормальное ускорение. Модули этих ускорений:
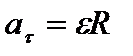 ,
, 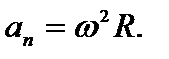
Модуль полного ускорения 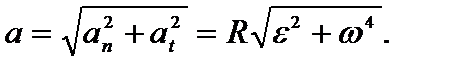
Дата добавления: 2015-04-01; просмотров: 2482;
