Преобразования Галилея.
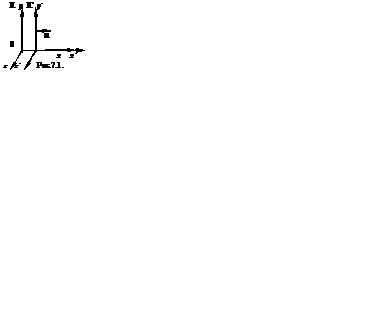 В механике Ньютона все законы выполняются в инерциальных системах отсчета. Пусть имеем две инерциальные системы отсчета, одну из которых мы будем условно считать неподвижной (система К с осями декартовых координат х ,у, z). Другая же система (система К’ с осями декартовых координат х’, у’, z’) пусть равномерно и прямолинейно движется со скоростью
В механике Ньютона все законы выполняются в инерциальных системах отсчета. Пусть имеем две инерциальные системы отсчета, одну из которых мы будем условно считать неподвижной (система К с осями декартовых координат х ,у, z). Другая же система (система К’ с осями декартовых координат х’, у’, z’) пусть равномерно и прямолинейно движется со скоростью 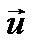 относительно первой (см. рис.7.1).
относительно первой (см. рис.7.1).
Примем для простоты, что оси х и х’ совпадают, а скорость относительного движения 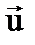 направлена вдоль оси х или х’. Пусть по часам наблюдателя в системе К прошло некоторое время t. В классической физике аксиоматически принимается, что такое же время зарегистрирует и наблюдатель в системе К’, т.е.
направлена вдоль оси х или х’. Пусть по часам наблюдателя в системе К прошло некоторое время t. В классической физике аксиоматически принимается, что такое же время зарегистрирует и наблюдатель в системе К’, т.е. 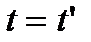 (1)
(1)
Если в момент времени, равный t=0, начало координат обеих систем совпадали, то за время t система К’ переместится на расстояние, равное 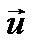 t. Пусть теперь в момент t’ в системе К’ в точке с координатами х’, у’, z’ произошло событие – включение электрической лампочки. Координаты лампочки, измеренные в момент
t. Пусть теперь в момент t’ в системе К’ в точке с координатами х’, у’, z’ произошло событие – включение электрической лампочки. Координаты лампочки, измеренные в момент 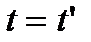 наблюдателем в системе К, имеют значение х, у, z. Видно, что между координатами в системах К и К’ легко устанавливается связь:
наблюдателем в системе К, имеют значение х, у, z. Видно, что между координатами в системах К и К’ легко устанавливается связь:
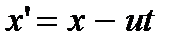 (2)
(2)
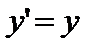 (3)
(3)
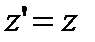 (4)
(4)
Соотношения (1)-(4) называются преобразованиями Галилея Преобразования Галилея связывают координаты и время события в указанных двух инерциальных системах отсчета. В векторной форме:
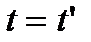
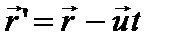 (5)
(5)
Дифференцируя (5) по времени, получим классический закон сложения скоростей: 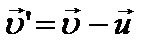 или
или 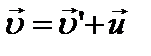
Продифференцируем его по времени и учтем, что 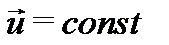 . Получим:
. Получим:
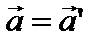 (6)
(6)
В классической механике считается, что масса тела не зависит от системы отсчета, то есть 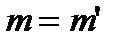 . Умножим обе части равенства (6) на m:
. Умножим обе части равенства (6) на m:
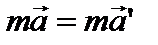 или
или 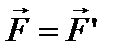
Таким образом, закон Ньютона не изменяется при переходе от системы К в систему К’.
На этом основании можно сформулировать механический принцип относительности Галилея: во всех инерциальных системах отсчета одни и те же механические явления протекают одинаковым образом, и никакими механическими опытами, проводимыми внутри данной инерциальной системы отсчета, невозможно установить, покоится система отсчета или движется равномерно и прямолинейно.
Физические величины и физические законы, не изменяющиеся при переходе от одной инерциальной системы отсчета к другой, называют инвариантными (не изменяющимися) к преобразованиям Галилея.
Дата добавления: 2015-04-01; просмотров: 1699;
