Решение. 1. Составим диагональную таблицу разностей, а затем, приведём её к треугольному виду и проанализируем
1. Составим диагональную таблицу разностей, а затем, приведём её к треугольному виду и проанализируем. В первую очередь отметим, что нумерация аргументов, значений функции и разностей во всех столбцах начинается с i=0.
Отсутствие смены знаков в столбце 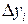 означает отсутствие экстремумов на исследуемом интервале, а о смене знаков в столбце
означает отсутствие экстремумов на исследуемом интервале, а о смене знаков в столбце 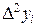 можно судить по наличию точек перегиба графика на указанном промежутке[2]. Необходимо отметить, что абсолютные величины конечных разностей сначала убывают с увеличением их порядка (до
можно судить по наличию точек перегиба графика на указанном промежутке[2]. Необходимо отметить, что абсолютные величины конечных разностей сначала убывают с увеличением их порядка (до 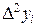 включительно), а затем возрастают. Это связано в первую очередь с ограниченной точностью задания значений табличной функции.
включительно), а затем возрастают. Это связано в первую очередь с ограниченной точностью задания значений табличной функции.
| i | 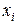
| 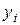
| 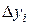
| 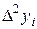
| 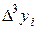
| 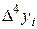
| 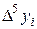
|
| -9,5 -4,5 0,5 5,5 10,5 15,5 | -11,971 -7,973 -3,614 1,928 6,872 11,972 | 3,998 4,359 5,542 4,944 5,1 | 0,36 1,183 -0,598 0,156 | 0,823 -1,782 0,755 | -2,604 2,536 | 5,141 |
2. По таблице разностей находим, что точки принадлежат интервалам: 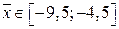 ;
; 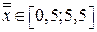 ;
; 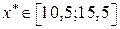 . Видно, что для точки
. Видно, что для точки 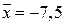 целесообразно выбрать в качестве базового узла
целесообразно выбрать в качестве базового узла 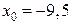 ; для
; для 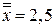 —
— 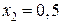 ; для
; для 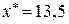 , соответственно
, соответственно 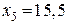 . При
. При 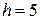 , получаем соответствующие новые переменные для каждой точки:
, получаем соответствующие новые переменные для каждой точки: 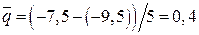 ;
; 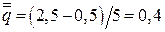 ;
; 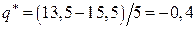 .
.
3. Для точки 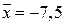 применяем интерполяцию вперед, т.е. первую формулу Ньютона (24)
применяем интерполяцию вперед, т.е. первую формулу Ньютона (24)
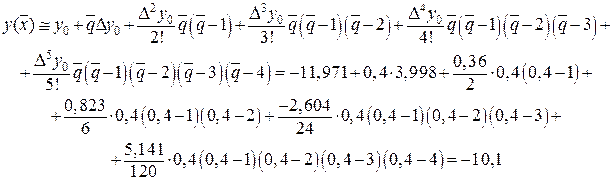 Для точки
Для точки 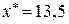 применяем интерполяцию назад, т.е. вторую формулу Ньютона (32)
применяем интерполяцию назад, т.е. вторую формулу Ньютона (32)
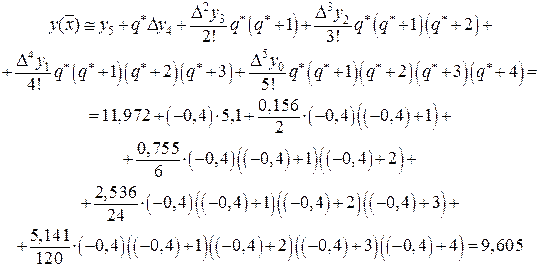
Для точки 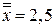 можно применить одну из центральных интерполяций (37), (38). По формуле Стирлинга (37)
можно применить одну из центральных интерполяций (37), (38). По формуле Стирлинга (37)
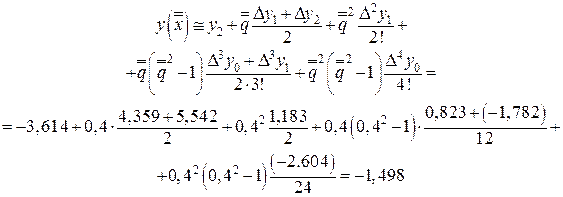
По формуле Бесселя (38)
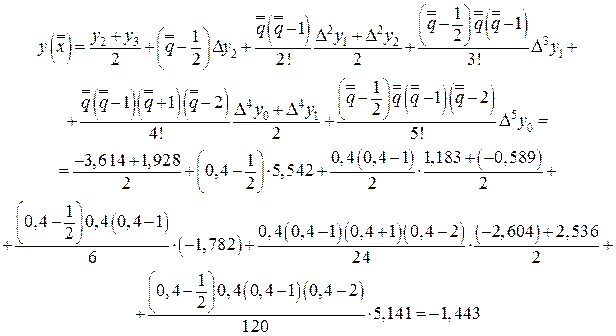
Главное преимущество конечноразностных интерполяций по сравнению с интерполяцией Лагранжа состоит в том, что здесь для увеличения точности вычисления просто добавляются слагаемые более высокого порядка, а не проделываются заново все вычисления.
Дата добавления: 2015-04-25; просмотров: 1117;
