Второй интерполяционный многочлен Ньютона

Записав (21) в другом виде

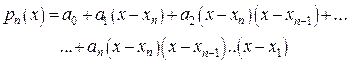(28)

и проделав аналогичную процедуру подстановки 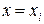в обратном порядке, начиная с i=n, можно получить второй интерполяционный многочлен Ньютона с коэффициентами

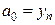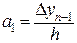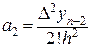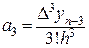; ; ; (29)

или в общем случае

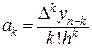. (30)

Подставляя (29), (30) в (28), получаем искомое разложение

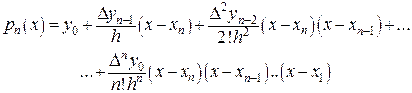(31)

Аналогично предыдущему случаю введем новую переменную 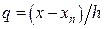, учтем, что 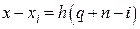, и в итоге запишем (31) в более удобной форме

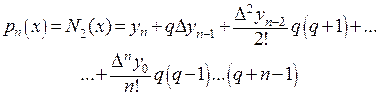(32)

называемой второй интерполяционной формулой Ньютона.

Проанализируем полученные соотношения.

На диагональной таблице разностей направления интерполяции в форме Ньютона показаны сплошными стрелками, поэтому, первую формулу (26) называют обычно интерполяцией вперед, а вторую (32) – интерполяцией назад. Узел, относительно которого строится интерполяционный многочлен, называется базовым. Таким образом, выбор базового узла обусловлен лишь требованиями близости значения к 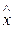, для которого необходимо вычислить значение функции в одном из узлов, а следовательно при этих условиях значение 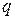будет по модулю заведомо меньше единицы. Выбор направления интерполяции (вперед или назад) зависит от заполнения диагональной таблицы разностей. 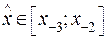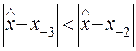Так, например, если и , то целесообразно выбрать базовым узел 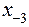и осуществить интерполяцию вперед по первой формуле Ньютона

,

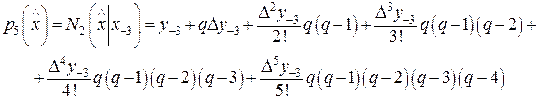где .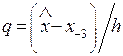

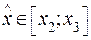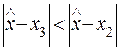Если и , то целесообразно выбрать базовым узел 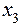и осуществить интерполяцию назад по второй формуле Ньютона

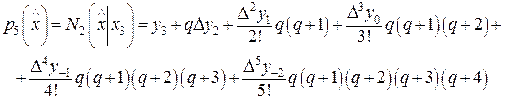
где 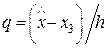и обозначили 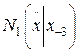, 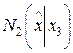показав базовые узлы.

Исходя из этого можно утверждать, что формулы Ньютона целесообразно применять тогда, когда заданное значение аргумента находится в начале или в конце таблицы.