Форма Лагранжа
Пусть на отрезке [a,b] заданы n+1опорных (узловых) точек 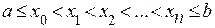 . Пусть, кроме того, заданы n+1 действительных чисел yj (j=0,1,……n) – значения функции. Тогда имеем следующую задачу интерполяции: найти многочлен
. Пусть, кроме того, заданы n+1 действительных чисел yj (j=0,1,……n) – значения функции. Тогда имеем следующую задачу интерполяции: найти многочлен 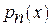 степени не больше n такой, что
степени не больше n такой, что 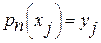 для
для 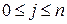 .
.
Данная интерполяция применяется тогда, когда известны только дискретные значения в узловых точках таблично заданной функции f(x), и для того, чтобы вычислить другие ее значения между (inter) точками или вне (extra) отрезка узловых точек. Найти многочлен 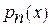 - это значит найти все его n+1 коэффициентов
- это значит найти все его n+1 коэффициентов 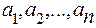
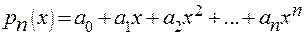 (3)
(3)
Условия 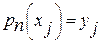 определяют систему n уравнений:
определяют систему n уравнений:
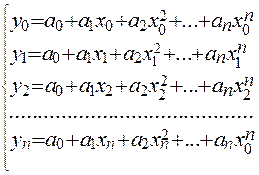 (4)
(4)
Она имеет единственное решение, ввиду того, что определитель Ван-дер-Монда системы
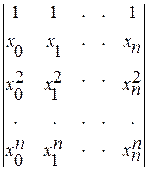
отличен от нуля. Решение этой системы уравнений представляет определенные сложности. Поэтому поступим следующим образом: будем строить многочлен n-ой степени  в виде линейной комбинации
в виде линейной комбинации  многочленов той же степени. Приравнивая
многочленов той же степени. Приравнивая 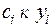 , а базисные многочлены символу Кронекера имеем:
, а базисные многочлены символу Кронекера имеем:
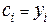
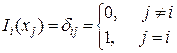 для " i, j. (5)
для " i, j. (5)
получаем
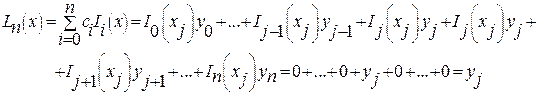
т.е. выполнено условие 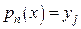 .
.
Теперь подберем многочлен 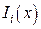 удовлетворяющий условию (5). Равенство нулю любого
удовлетворяющий условию (5). Равенство нулю любого 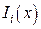 во всех узлах, кроме i-го, можно обеспечить, записав его в виде
во всех узлах, кроме i-го, можно обеспечить, записав его в виде
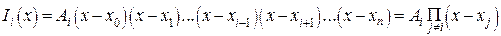 (6)
(6)
Так как, в соответствии с (5), 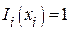 , то из последнего выражения определяется нормировочный коэффициент
, то из последнего выражения определяется нормировочный коэффициент 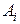 :
:
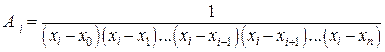 (7)
(7)
Подставляя (7) в (6), получим для базисного многочлена в форме Лагранжа
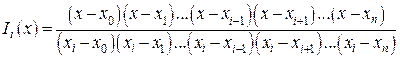 (8)
(8)
и в результате искомый многочлен есть
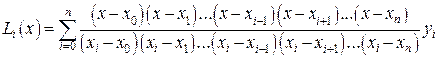 (9)
(9)
Рассмотрим в качестве примеров первые три интерполяционные формулы.
Линейная интерполяция (n=1).
Для этого случая имеется информация о f(x) в двух точках (x0,y0) и (x1,y1). Очевидно, что искомый многочлен есть прямая проходящая через указанные точки, и определяется она с помощью двух базисных многочленов первой степени 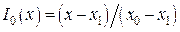 и
и 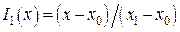 . Тогда
. Тогда
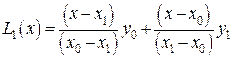 (10)
(10)
Пример 1. Рассмотрим линейную интерполяцию функции 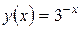 на отрезке [0;6] по двум крайним точкам интервала y(0)=1, y(6)=1/729.
на отрезке [0;6] по двум крайним точкам интервала y(0)=1, y(6)=1/729.
По формуле (10) получаем
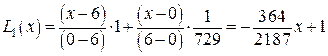 (10*)
(10*)
Квадратичная интерполяция (n=2).
Теперь информация о функции f(x) имеется в трех точках, приведённых в таблице
| i | |||
| xi | x0 | x1 | x2 |
| yi | y0 | y1 | y2 |
По трем базисным многочленам:
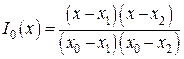 ,
, 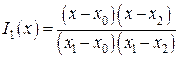 ,
, 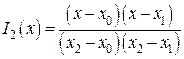
образуется квадратичная интерполяция
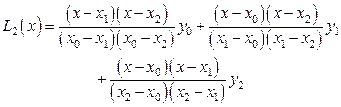 (11)
(11)
Пример 2. Рассмотрим квадратичную интерполяцию той же функции 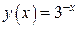 на отрезке [0;6] по трем точкам: y(0)=1, y(3)=1/27, y(6)=1/729. По (11) получаем
на отрезке [0;6] по трем точкам: y(0)=1, y(3)=1/27, y(6)=1/729. По (11) получаем
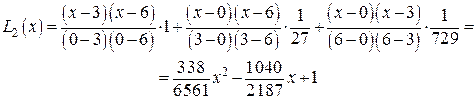 (11*)
(11*)
Кубическая интерполяция (n=3).
Здесь образование интерполяционного многочлена осуществляется по четырем точкам
| i | ||||
| xi | x0 | x1 | x2 | x3 |
| yi | y0 | y1 | y2 | y3 |
По формуле (9), записывая аналогично выражения для базисных многочленов, получаем
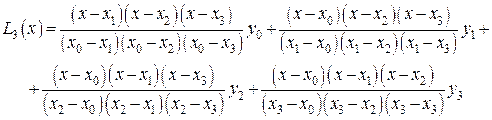 (12)
(12)
Пример 3. Рассмотрим кубическую интерполяцию той же функции 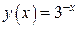 на отрезке [0;6] по четырем точкам: y(0)=1, y(2)=1/9, y(4)=1/81, y(6)=1/729. По формуле (12) получаем
на отрезке [0;6] по четырем точкам: y(0)=1, y(2)=1/9, y(4)=1/81, y(6)=1/729. По формуле (12) получаем
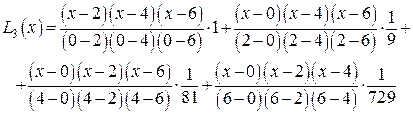
или после преобразований
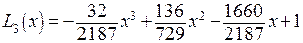 (12*)
(12*)
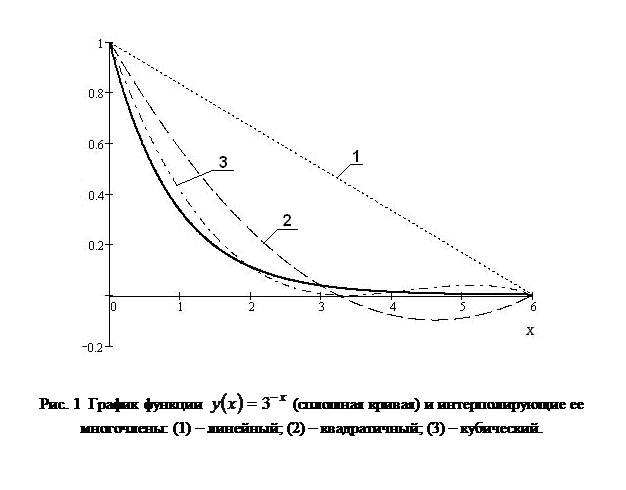 Полученные приближения наглядно иллюстрируют графики зависимостей (10 - 12*) построенные на рис. 1. Даже без соответствующих оценок видно, что кубическая интерполяция лучше описывает заданную функцию по сравнению с линейной и квадратичной.
Полученные приближения наглядно иллюстрируют графики зависимостей (10 - 12*) построенные на рис. 1. Даже без соответствующих оценок видно, что кубическая интерполяция лучше описывает заданную функцию по сравнению с линейной и квадратичной.
Теперь оценим погрешность полученных приближений. По формуле (1) получаем:
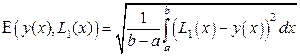 , (13)
, (13)
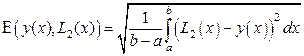 , (14)
, (14)
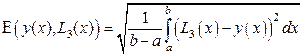 , (15)
, (15)
где а и b – границы отрезка [0,6].
Интегралы (13)-(15) вида 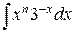 вычисляем в элементарных функциях. Интегрируя (13)-(15), получаем:
вычисляем в элементарных функциях. Интегрируя (13)-(15), получаем:
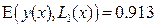
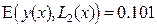
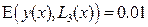
Из чего следует, что из трёх полученных аппроксимаций наиболее точно исходную функцию 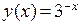 описывает кубическая аппроксимация
описывает кубическая аппроксимация 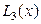 .
.
Для получения приближенных значений из отрезка [a;b] выберем внутри исследуемого интервала контрольную точку 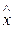 и сравним значения функции с ее аппроксимациями. Пусть
и сравним значения функции с ее аппроксимациями. Пусть 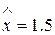 . Подставляя
. Подставляя 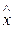 в (10*)-(12*) и вычисляя по таблицам значение функции, получаем:
в (10*)-(12*) и вычисляя по таблицам значение функции, получаем: 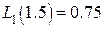 ,
, 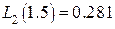 ,
, 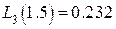 , а
, а 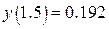 . Ошибка вычисления по формуле
. Ошибка вычисления по формуле 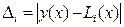 составит:
составит: 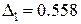 ,
, 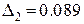 ,
, 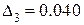 . Откуда видно, что при наибольшем n ошибка минимальна, т.е. при кубической интерполяции.
. Откуда видно, что при наибольшем n ошибка минимальна, т.е. при кубической интерполяции.
Другой способ получить общую оценку (в произвольной точке) - из выражения для остаточного члена
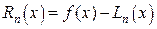
т.е. отклонения 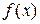 от
от 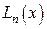 . Считая, что
. Считая, что 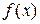 на [a,b] непрерывно дифференцируема n+1 раз можно показать, что максимальная погрешность на этом интервале оценивается величиной
на [a,b] непрерывно дифференцируема n+1 раз можно показать, что максимальная погрешность на этом интервале оценивается величиной
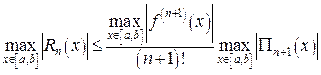 (16)
(16)
где обозначено
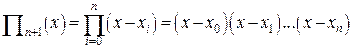
Из формулы (16) следует, что остаточный член с увеличением n уменьшается, следовательно, при этом выполняется условие 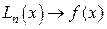 , т.е. возрастает точность интерполяции.
, т.е. возрастает точность интерполяции.
Достоинством формулы Лагранжа, безусловно, является отсутствие каких-либо требований к расстояниям между узловыми точками, однако для практических вычислений она неудобна, так как при переходе к более высоким степеням многочлена приходится заново вычислять все входящие в него слагаемые. Поэтому чаще применяются полиномиальные интерполяции в более удобном разложении, при котором каждое следующее слагаемое просто добавляется к уже вычисленным.
Дата добавления: 2015-04-25; просмотров: 2581;
