Конечноразностные формулы
Рассмотрим наиболее простой и часто применяемый случай равноотстоящих интерполяционных точек, т.е. когда 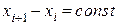 для любого
для любого 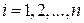 . Тогда можно построить другие интерполяционные многочлены, использующие понятие разностей функции. Величина
. Тогда можно построить другие интерполяционные многочлены, использующие понятие разностей функции. Величина 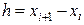 в этом случае называется ступенью (или шагом) заданной таблицы значений
в этом случае называется ступенью (или шагом) заданной таблицы значений 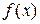 ;
; 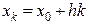 . (Это обозначение сохраняется и при k<0.)
. (Это обозначение сохраняется и при k<0.)
Первые разности функции по отношению к данному шагу h определяются формулами
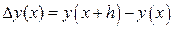 ,
, 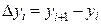 (17)
(17)
Разности первых разностей образуют разности второго порядка (или вторые разности):
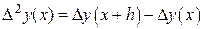 ,
, 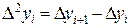 (18)
(18)
Так же определяются и разности более высоких порядков и описываются рекуррентной формулой
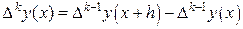 ,
, 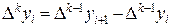 (19)
(19)
Из формул (17) - (18) можно установить связь между конечными разностями и значениями функций. Эта связь выражается общей формулой
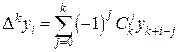 (20)
(20)
где 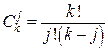 - число сочетаний из n различных элементов по m, которые можно определить непосредственно вычислением, или из так называемого треугольника Паскаля:
- число сочетаний из n различных элементов по m, которые можно определить непосредственно вычислением, или из так называемого треугольника Паскаля:
| n | Коэффициенты |
| 1 1 | |
| 1 2 1 | |
| 1 3 3 1 | |
| 1 4 6 4 1 | |
| 1 5 10 10 5 1 | |
| 1 6 15 20 15 6 1 |
Для первых порядков разностей
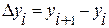
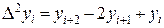
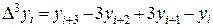
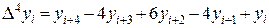
Для функции 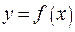 , заданной таблицей своих значений
, заданной таблицей своих значений 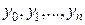 в равноотстоящих узлах
в равноотстоящих узлах 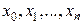 конечные разности разных порядков удобно сводить в общую таблицу с узлами и значениями функции. (См. ниже).
конечные разности разных порядков удобно сводить в общую таблицу с узлами и значениями функции. (См. ниже).
Диагональная таблица разностей
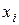
| 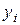
| 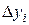
| 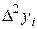
| 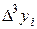
| 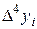
| 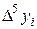
| |
…
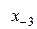
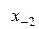
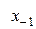
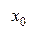
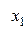
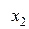
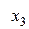 …
…
| …
 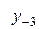
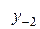
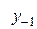
   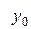
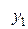
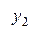
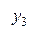 …
…
|
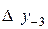
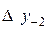
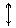 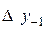
 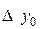
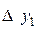
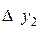
|
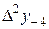
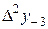
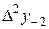
 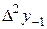
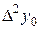
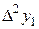
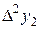
|
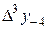
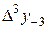
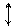 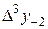
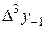
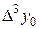
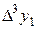
|
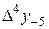
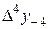
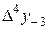
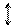 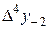
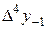
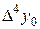
|
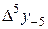
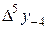
 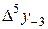
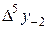
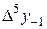
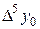
|
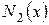
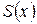
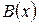
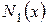
|
В этой таблице всякое число является разностью двух чисел предыдущего столбца, стоящих на полстроки ниже и на полстроки выше рассматриваемого. При составлении таблицы разностей следует иметь в виду, что наличие в первом столбце ошибок, не превышающих e по абсолютной величине, может привести к ошибкам, доходящим до 2e во втором, 4e в третьем, 2m+1e в m-м столбце. Поэтому даже незначительные погрешности в значениях функции могут сильно повлиять на разности высших порядков. Вычисления разностей следует прекращать, если все числа некоторого столбца оказываются почти равными между собой. На основании таблицы можно построить ряд так называемых конечноразностных интерполяционных формул, которые будем искать в виде полинома
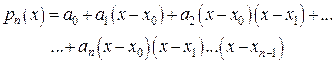 (21)
(21)
где коэффициенты 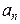 определяются из условий
определяются из условий 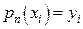 . Подставляя в (21)
. Подставляя в (21) 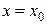 , получаем
, получаем 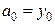 .
.
Дата добавления: 2015-04-25; просмотров: 1129;
