Полиномиальные интерполяции
Весьма редко удается решить задачу прямыми аналитическими методами, тем более реализовать решение в виде вычислительного алгоритма. Основными требованиями к алгоритму являются:
- изменяемость в зависимости от начальных (исходных) условий, т.е. путь решения должен быть по возможности универсальным;
- схематизированность (однозначно должна быть определена последовательность действий),
- рекурсированность – рекурсированный алгоритм состоит из небольших частей, которые неоднократно реализуются для различных наборов значений;
- решение, реализуемое алгоритмом должно быть конечным, т.е. должно приводить к конечному результату за конечное число шагов. Другими словами, не должно существовать различного рода расходимостей (например, часто встречаются т.н. логарифмические расходимости вида 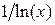 , разрывы первого и второго родов, скачки значений производных и т.д.), которые могут оказать существенное влияние на конечный результат. Поэтому реализации алгоритма непосредственно на ЭВМ должен предшествовать тщательный анализ задачи с целью выявления различных особенностей в поведении исследуемого процесса.
, разрывы первого и второго родов, скачки значений производных и т.д.), которые могут оказать существенное влияние на конечный результат. Поэтому реализации алгоритма непосредственно на ЭВМ должен предшествовать тщательный анализ задачи с целью выявления различных особенностей в поведении исследуемого процесса.
Последнее требование представляется авторам наиболее важным с точки зрения достоверности получаемых результатов вычисления.
Часто при обработке статистических данных возникает задача замены аналитического описания некоторого реального процесса на другое, более удобное с точки зрения дальнейших математических преобразований. Т.е. мы заменяем некоторую функцию f(x) (известную, неизвестную, частично известную), другой ψ(x), полученной в результате некоторых преобразований. В зависимости от цели исследования выбирается метод интерполяции[1] или экстраполяции - процесс построения приближенного или аппроксимирующего многочлена соответственно внутри и вне промежутка исследования. Так как методики интерполяции и экстраполяции практически не отличаются друг от друга, то в дальнейшем будем ограничиваться примерами интерполяции. В связи с этим вышеупомянутую процедуру должен предварять анализ исходной зависимости f(x), а именно:
1. Способ и интервал задания функции (аналитический или табличный);
2. Оценка степени гладкости функции, имеется ли возможность определения производных;
3. Требования к интерполирующей функции ψ(x) (определение ее класса);
4. Определение критерия качества интерполяции, иначе говоря, задание способа оценки погрешности интерполяции. Необходимо в первую очередь определить источники погрешностей. Чаще всего наиболее существенное влияние оказывают следующие:
— погрешность исходных данных;
— погрешность метода;
— погрешность округления;
Погрешность исходных данных, как правило, легче всего поддается оценке и соответствующей корректировке. Более того, часто удается получить точную аналитическую формулу ошибок, исходя из выводов теории вероятностей и математической статистики.
Так как вычислительный алгоритм является рекурсивным, состоящим из целого ряда операций, то происходит т.н. накопление погрешностей: погрешности результата каждого шага оказываются исходными для следующей операции, поэтому точный анализ погрешностей оказывается трудновыполнимым и приходится ограничиваться доверительными оценками.
Сформулируем основные положения.
Первое. Будем рассматривать как таблично, так и аналитически заданные функции.
Второе. В основном будем использовать полиномиальную или кусочно-полиномиальную интерполяцию, т.е. рассматривать в качестве аппроксимирующих функций ψ(x) только многочлены. Данная форма ψ(x) выглядит в большинстве случаев более предпочтительной с точки зрения упрощения дальнейших математических действий (дифференцирования, интегрирования). Другие виды приближений (тригонометрическое, экспоненциальное и пр.) будут применены в следующих разделах.
Третье. Построение аппроксимирующего многочлена и оценку погрешности будем производить с помощью функционалов
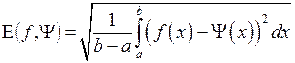 (1)
(1)
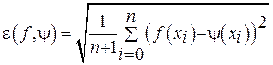 (2)
(2)
соответственно для непрерывных и дискретных функций. Оценка погрешности (степени близости функций f(x) и ψ(x)) по формулам (1) и (2) смысл среднеквадратичной погрешности.
Будем называть вычислительный метод устойчивым, если для любого 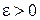 существует такое
существует такое 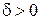 , что максимальная погрешность результата вычислений меньше
, что максимальная погрешность результата вычислений меньше 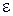 при максимальной погрешности исходных данных меньше
при максимальной погрешности исходных данных меньше 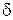 .
.
Дата добавления: 2015-04-25; просмотров: 1282;
