Полиномиальные методы

Полиномиальные способы предполагают представление модели­руемой поверхности полиномом второй - пятой степени вида

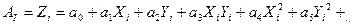(5.8)

Для отыскания неизвестных коэффициентов полинома для каждой опорной точки составляют одно уравнение поправок вида

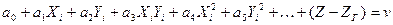(5.9)

где свободный член (Z – Z_Г) представляет собой уклонение вычислен­ной по формуле (5.7) отметки (Z) с приближенными значениям ко­эффициентов полинома от исходной (Z_Г). Полученную систему реша­ют последовательными приближениями, в каждом из которых неизве­стные находят методом наименьших квадратов, под условием [pv 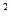]= min. Найденные таким образом коэффициенты а₀...а_i уравнений (5.7) используют для интерполяции высот точек, расположенных в области моделирования.

Кусочно-полиномиальные способы предполагают деление области моделирования на участки, подбор для каждого участка своего ло­кального полинома вида (5.7) и последующую связь локальных поли­номов с помощью переходных уравнений. Во всех случаях возникают переопределенные системы, которые решаются под условием миниму­ма суммы квадратов расхождений высот точек реальной и аппроксими­рующей поверхностей.

Сходные по характеру решения используют способы, основанные на применении рядов Фурье (разложений по сферическим гармони­кам), различного рода сплайнов (кубических, бикубических, на много­образиях и др.) и т. п. [3].

На русский язык термин "spline" переводится как "гибкая рейка" или "плавная кривая" [5].

Сплайны используются для сглаживания линий при отображении гладких поверхностей (поле и т.д.).