Пространственная триангуляция Делоне

Задача построение сети неперекрывающихся треугольников является одной из базовых в вычислительной геометрии и широко используется в машинной графике и геоинформационных системах для моделирования поверхности и решения пространственных задач.

Впервые задача построения сети неперекрывающихся треуголь­ников была поставлена в 1934 году в работе советского математика Б. Н. Делоне, который сформулировал и соответствующие условия.

В математике задачей построения триангуляции по заданным точкам называют задачу их попарного соединений непересекающимися отрезками так, чтобы образовалась сеть треугольников. Основными ее элементами являются (рис.5.3): узлы (вершины треугольников), ребра (стороны) и грани (собственно треугольники). Построенная три­ан­гуляция может быть выпуклой (если таковым будет минимальный многоугольник, охватывающий область моделирования), невыпуклой (если триангуляция не является выпуклой) и оптимальной (если сумма длин всех ребер минимальна).

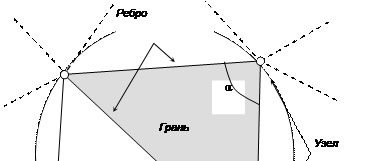Сеть таких треугольников называется триангуляцией Делоне, если она удовлетворяет некоторым условиям:

• внутрь окружности, описанной вокруг любого треугольника, не попадает ни одна из исходных точек (рис. 5.3);

• триангуляция является выпуклой и удовлетворяет сформулиро­ванному выше условию Делоне;

• сумма минимальных углов всех треугольников максимальна из всех возможных триангуляций;

• сумма радиусов окружностей, описанных около треугольников, минимальна среди всех возможных триангуляций [2].

Первый из названных выше критериев построения триангуляции Делоне, называемый круговым, является одним из основных и проверяется для любой пары треугольников с общими гранями. Математическая интерпретация критерия вытекает из рис. 5.3:

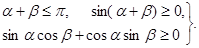(5.2)

Существует множество способов построения триангуляции Делоне, которая является одним из самых популярных в последнее время способов построения триангуляционной сетки. Она применяется во многих ГИС системах для построения моделей рельефа.

В приложении к двумерному пространству она формулируется следующим образом: система взаимосвязанных неперекрывающихся треугольников имеет наименьший периметр, если ни одна из вершин не попадает внутрь ни одной из окружностей, описанных вокруг образованных треугольников (рис. 5.4).

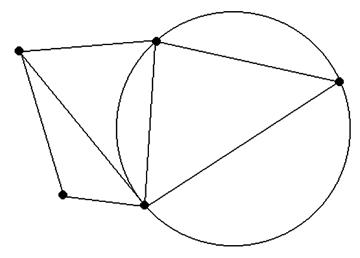
Рис. 5.4. Триангуляция Делоне

Это означает, что образовавшиеся треугольники при такой триангуляции максимально приближаются к равносторонним, а каждая из сторон образовавшихся треугольников из противолежащей вершины видна под максимальным углом из всех возможных точек соответствующей полуплоскости. Это именно та оптимальная триангуляция, по ребрам которой делается обычно линейная интерполяция для построения изолиний.

Многие алгоритмы построения триангуляции Делоне используют следующую теорему [4].

Теорема 1. Триангуляцию Делоне можно получить из любой другой триангуляции по той же си­стеме точек, последовательно перестраивая пары соседних треугольников ABC и BCD, не удовлетво­ряющих условию Делоне, в пары треугольников ABD и ACD (рис. 5.5).

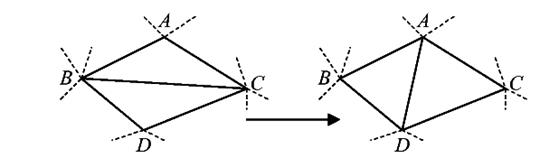
Рис. 5.5.. Перестроение треугольников, не удовлетворяющих условию Делоне

Такую операцию перестроения часто называют флипом. Данная теорема позволяет строить три­ангуляцию Делоне последовательно, вначале строя некоторую триангуляцию, а потом последовательно улучшая ее в смысле условия Делоне. При проверке условия Делоне для пар соседних треугольников можно использовать непосредственно определение, но иногда используются другие способы, основанные на условиях, перечисленных выше.

В данных условиях фигурирует суммарная характеристика всей триангуляции (сумма мини­мальных углов или сумма радиусов), оптимизируя которую можно получить триангуляцию Делоне.

Как было сказано выше одна из важнейших операций, выполняемых при построении три­ангуляции, является проверка условия Делоне для заданных пар треугольников. На основе определения триангуляции Делоне и соответствующих условий на практике обычно используют несколько способов проверки:

– проверка через уравнение описанной окружности;

– проверка с заранее вычисленной описанной окружностью;

– проверка суммы противолежащих углов;

– модифицированная проверка суммы противолежащих углов.

В многих системах выполняется проверка с заранее вычисленной описанной окружностью. Основная идея алгоритма проверки через за­ранее вычисленные окружности заключается в предварительном вычислении для каждого построенного треугольника центра и радиуса описанной вокруг него окружности, после чего проверка условия Делоне будет сводиться к вычислению расстояния до центра этой окружности и сравнению результата с ради­усом. Центр 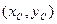и радиус r окружности, описанной вокруг 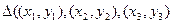можно найти как 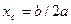, , 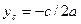, 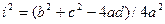r² = (b² + с² - 4аd)/4а², где значения а, b, с, d определены по формулам 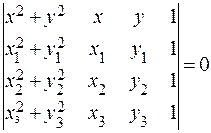(5.3)

(5.3)

Другая запись уравнения этой окружности имеет вид:

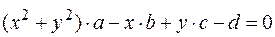(.5.4)

где:

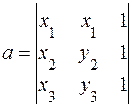
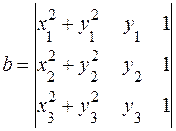(5.5.)

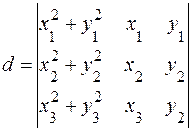
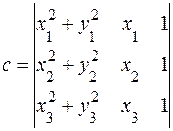(5.6)

Тогда условие Делоне для 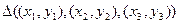будет выполняться только тогда, когда для любой другой точки 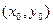триангуляции будет:

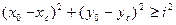(x₀ – x_C)² + (y₀ – y_C)² ≥ r² . (5.7)

В настоящее время существует множество алгоритмов построения триангуляции Делоне. Многие из известных алгоритмов используют определение триангуляции Делоне как вторичный признак триангуляции. Поэтому в таких алгоритмах отмечаются следующие слабости:

– алгоритмы используют постоянно вычисляемые тригонометрические функции, что резко замедляет процесс;

– при исследовании взаимоотношения точек и базового отрезка возникают очень малые углы, и при использовании тригонометрических функций постоянно появляется опасность исчезновения порядка и деления на 0 в связи с ограниченной точностью представлений данных в компьютере, эта ситуация требует постоянной дополнительной обработки [4].

Наиболее известные программные продукты строят триангуляцию Делоне, используя теорему о пустом шаре как основной, первичный принцип построения треугольников. Алгоритм выглядит так:

– все множество точек делится на треугольники, т.е. создаются комбинации из трех точек;

– для каждой комбинации находится описанная окружность и координаты ее центра;

– если внутри окружности текущей комбинации не находится ни одной точки из оставшихся то эта комбинация есть треугольник – часть триангуляции Делоне.

К достоинствам этого алгоритма можно отнести:

– отсутствие использования тригонометрических функций, что не замедляет процесс построений;

– непосредственное построение триангуляции Делоне, без каких – либо предварительных построений;

– простота всех вычислений и преобразований;

– в итоге триангуляционная сетка представлена множеством треугольников, а не отдельных линий.

Построенная таким образом триангуляция является геометрической основой для построения изолиний.

Алгоритмы построения триан­гу­ляции Делоне можно разделить на ряд групп, различающиеся структурой используемых входных данных, объемом вычис­ли­тель­ных операций, исходными пред­по­сылками и др. Рассмотрим некоторые из них.

Алгоритмы слияния предполагают разбиение множества исход­ных точек на подмножества, построение на каждом из них триан­гуляции и последующее их объединение в единую сеть. Сущ­ность одного из таких алгоритмов сводится к следующему.

Множество исходных точек делится вертикальными линиями на две или более частей, после чего каждая из них разделяются горизонтальными и вертикаль­ными линиями на примерно равные части. В результате вся область исходных точек оказывается разделенной на примитивы по три – четыре точки (рис. 2.4), по которым строятся один – два треугольника.

Слияние этих треугольников в единую сеть выполняется путем построения двух базовых линий (P₀P₁ и P₂P₃, рис. 5,7.а), проведении окружностей переменного радиуса с центром на серединном перпендикуляре к базовой линии (рис. 5.7, б), поиску попадающего на окружность узла (точка A, рис. 5.7. в) и построению нового треугольника (P₀P₁A). При этом может возникнуть необходимость удаления уже существующего треугольника (например, P₀AB).

Итеративные алгоритмы основаны на идее последовательного добавления точек в частично построенную триангуляцию с одновременным ее улучшением и перестроением в соответствии с критериями Делоне. В общем виде они включают несколько шагов и сводятся к построению треугольника на первых трех исходных точках и исследованию нескольких вариантов размещения очередной точки. В частности, рассматриваются варианты ее попадания за границу области моделирования, на существующий узел или ребро, внутрь построенного треугольника и др. Каждый из этих вариантов предполагает выполнение определенной операции: разбивки ребра на два, грани – на три и т.д.; после чего выполняется проверка полученных треу­голь­ников на соответствие условию Делоне и необходимые перестроения.

Двухпроходные алгоритмы, предусматривают вначале построение некоторой триангуляции, игнорируя условия Делоне, а затем – ее перестроение в соответствии с этими условиями. Пример при­менения алгоритма приведен на рис. 5.8.

Для приближения создаваемой модели рельефа к реальной в нее внедряются дополнительные элементы, обеспечивающие учет и отображение ее линейных и площадных структурных элементов. Такими дополнительными элементами являются широко используе­мые в топографии структурные линии, определяющие «скелет рельефа»: водоразделы, тальвеги, хребты, обрывы, уступы, озера, овраги, береговые линии, границы искусственных сооружений и др., совокупность которых создает как бы каркас триангуляции Делоне. Эти структурные линии внедряются в триангуляцию в качестве ребер треугольников, чем и достигается моделирование реальных элементов рельефа на фоне общих неровностей земной поверхности. Такие ребра называются структурными (фиксированными, неперестраиваемыми), не пересекают ребра других треугольников и в последующем не изменяются.

Задача построения модели поверхности с учетом структурных линий называется триангуляцией Делоне с ограничениями, если условия Делоне выполняются для любой пары смежных треугольников, которые не разделяются структурными линиями. Наиболее эффективно, считают исследователи, выполняется построение такой триангуляции с помощью итеративных алгоритмов.

Алгоритмы построения триангуляции Делоне реализуются с вещественным или целочисленным представлением координат узлов, что позволяет существенно повысить скорость и точность обработки, но порождает проблемы поиска и исключения совпадающих узлов.

Модель TIN легко редактируется путем перемещения узлов, вставки новых, удаления имеющихся, изменения положения одного или нескольких ребер, внедрения новых структурных линий и др. Такие изменения всегда затрагивают небольшую группу смежных треугольников, не требуют перестроения всей сети и осуществляются в режиме on-line, по указанию курсором на соответствующий элемент [2].

О точности:

Располагая пикеты на характерных элементах рельефа (например, водоразделах и тальвегах), мы игнорируем более мелкие элементы в промежутках. При построении горизонталей1 по таким ребрам треугольников возникает ошибка, которая зависит от величины неровности рельефа и угла наклона местности. Например, средняя погрешность съемки рельефа, не должна превышать 1/3 сечения рельефа при углах наклона поверхности от 2 до 10 градусов. Можно рассчитать, что при сечении рельефа 0,5 м предельная величина пропущенной неровности (то есть отклонения поверхности земли от прямой, проходящей через соседние пикеты) не должна превышать (0,5/3)*cos10°=0,16 м.

Для точности определения объема перемещаемого грунта важна также площадь, занимаемая не учитываемой деталью рельефа. Допустим, в квадрате 20х20 м между двумя парами пикетов имеется цилиндрическая выпуклость с максимальной высотой 0,15 м. Нетрудно подсчитать, что ее неучет при представлении данной поверхности только двумя треугольниками приведет к ошибке приблизительно в 40 м3. Не так уж много, но для участка в 1 га, расположенного на холме или верхней (как правило, выпуклой) части склона, получится уже 40*25=1000 м3 лишнего грунта. Если же брать пикеты в два раза чаще (то есть через 10 м), ошибка уменьшится вчетверо и составит 250 м3 на гектар. Этот фактор можно учесть заранее, поскольку положительные формы равнинного рельефа обычно имеют выпуклую форму, а отрицательные – вогнутую. Если на подлежащий съемке участок имеются приближенные данные о рельефе, то радиус кривизны поверхности и необходимую густоту пикетов легко рассчитать по величинам заложения горизонталей или отдельным высотным отметкам.

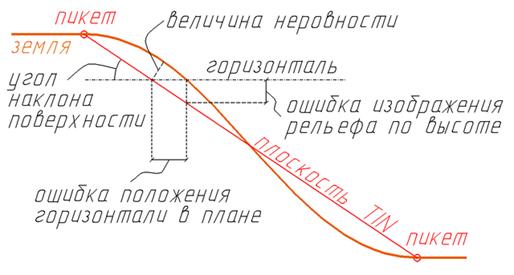
Рис 5.9.а