Математические модели местности

Математические связи между исходными точками цифровых моделей описываются линейными либо нелинейными (степенными) зависимостями. В первом случае связь между смежными точками модели описывается уравнениями плоскостей, проходящими через каждые три смежные точки модели, во втором — криволинейными поверхностями разного порядка, и, таким образом, рельеф местности задается либо множеством пересекающихся между собой плоскостей, либо поверхностей различной кривизны.

Решение наиболее актуальной задачи при математическом моделировании рельефа и инженерно-геологического строения местности заключается в определении высот точек местности, а также уровней грунтовых вод и соответствующих геологических напластований в пикетных и плюсовых точках по оси запроектированных вариантов трассы и на поперечниках.

Подавляющее число регулярных и нерегулярных ЦММ предполагают при последующем математическом моделировании линейную интерполяцию высот между смежными точками модели.

Задача определения высот точек трассы, уровней грунтовых вод и поверхностей геологических напластований сводится к нахождению в каждом случае тех трех смежных исходных точек модели, между которыми попадет соответствующая искомая точка трассы, в нахождении коэффициентов уравнения плоскости, проходящей через эти три точки, и наконец, в определении по полученному уравнению искомой высоты. (рис. 5.2).

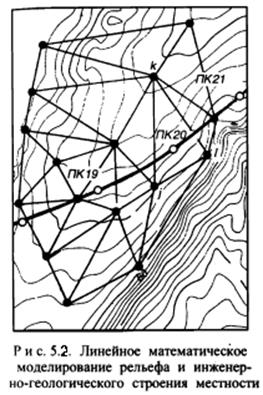
Если в уравнение (5.1) подставить известные координаты трех исходных точек цифровой модели, то получим три уравнения, в которых не известны только три коэффициента А, В и С:

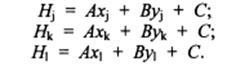(5.1)