XIV. Космическая триангуляция.
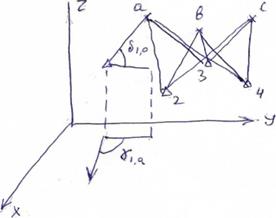
Идея такого построения принадлежит финскому геодезисту И.Вяйсяля (1946). Суть его заключается в том, что при одновременных фотографических наблюдениях ИСЗ с разных пунктов земной поверхности, по известным координатам некоторых из этих пунктов, можно вычислить координаты ИСЗ, и затем координаты определяемых пунктов.
Исходные данные:
Координаты пунктов на поверхности Земли и координаты ИСЗ.
Табл.17
| № п/п | Координаты | ||
| X | Y | Z | |
| 6101,000 | 20,000 | 0,300 | |
| 5501,000 | 40,000 | 0,250 | |
| 5901,000 | 70,000 | 0,200 | |
| 5789,004 | 70,004 | 0,160 | |
| a | 6399,000 | 1200,000 | 1350,000 |
| b | 7299,000 | 1360,000 | 1300,000 |
| c | 6999,000 | 1300,000 | 1330,000 |
Найти:
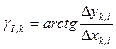 ;
; 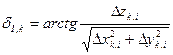 ;
;
k=a,b,c; i=1,2,3,4
Табл.18
| arctg(γ ki) | arct(δ ki) | |||||
| a | b | c | a | b | c | |
| 1,323426277 | 0,841289459 | 0,959022 | 0,837033 | 0,62605 | 0,704736 | |
| 0,912025066 | 0,633279083 | 0,699317 | 0,743806 | 0,527611 | 0,596717 | |
| 1,155696473 | 0,745241191 | 0,842039 | 0,829835 | 0,59943 | 0,678711 | |
| 1,075801367 | 0,706987602 | 0,793595 | 0,810341 | 0,579534 | 0,656647 |
Обратная задача.
Дано x1, x2, x3, y1, y2, y3, z1, z2, z3, γi,k, δi,k
Найти: xa, xb, xc, ya, vb, yc, za, zb, zc, x4, y4, z4.
Формулы Юнга:
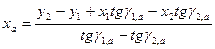 ;
;
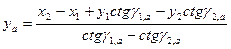 ;
;
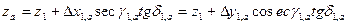
Табл.19
| через1-2 | через2-3 | через3-4 | через4-1 | |
| xa | ||||
| ya | ||||
| za | ||||
| za | ||||
| xb | ||||
| yb | ||||
| zb | ||||
| zb | ||||
| xc | ||||
| yc | ||||
| zc | ||||
| zc |
Дата добавления: 2015-06-10; просмотров: 2075;
