Произвольная пространственная система сил.
3.2.1. Момент силы относительно точки. Момент силы относительно оси. Теория пар в пространстве.
В случае плоской системы сил момент силы относительно точки определён как алгебраическая величина:  . При пространственном расположении сил этого определения не достаточно, так как плоскости, проходящие через линии действия сил и точку, относительно которой определяется момент, различны. Поэтому момент
. При пространственном расположении сил этого определения не достаточно, так как плоскости, проходящие через линии действия сил и точку, относительно которой определяется момент, различны. Поэтому момент 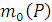 силы P относительно точки О в пространстве определяют как векторное произведение
силы P относительно точки О в пространстве определяют как векторное произведение  , где
, где  - вектор радиус проведенный из точки О в точку приложения силы.
- вектор радиус проведенный из точки О в точку приложения силы.
 Таким образом вектор
Таким образом вектор 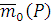 направлен перпендикулярно плоскости, содержащий линию действия силы и точку О, так что сила
направлен перпендикулярно плоскости, содержащий линию действия силы и точку О, так что сила  с конца его вектора
с конца его вектора 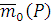 видно направление против часовой стрелки.
видно направление против часовой стрелки.
Рис. 1.40
Модуль вектора  равен:
равен:

Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.


Рис. 1.41
Если сила  с конца оси z видно направление вокруг точки О против часовой стрелки то момент положительный.
с конца оси z видно направление вокруг точки О против часовой стрелки то момент положительный.
Итак, момент силы относительно точки – вектор, а момент силы относительно оси – скалярная величина.
При вычислении моментов относительно оси надо иметь следующие частные случаи:
1. Если сила параллельна оси, то её момент относительно оси равен нулю 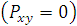 .
.
2. Если линия действия силы пересекает ось, то её момент относительно оси равен нулю 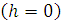 .
.
3. Если сила перпендикулярна оси, то её момент относительно оси равен произведению модуля силы на расстояние между силой и осью.
Получим аналитическое выражение для моментов силы относительно осей координат.

Рис. 1.42
Спроецируем силу 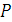 на плоскость
на плоскость  и разложим полученную проекцию на составляющие
и разложим полученную проекцию на составляющие 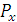 и
и  ; численно эти составляющие будут, очевидно, равны проекциям силы
; численно эти составляющие будут, очевидно, равны проекциям силы 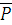 на оси
на оси 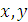 . Тогда
. Тогда

Последнее равенство вытекает из теоремы Вариньона. Но как видно из чертежа,  следовательно
следовательно 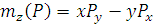 . Аналогично вычисляются моменты относительно других осей.
. Аналогично вычисляются моменты относительно других осей.
В результате получим:


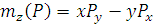
3.2.2. Зависимость между моментом силы относительно центра и относительно оси.

Рис. 1.43
Пусть на тело действует приложенная в точке  сила
сила 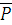 . Проведём ось
. Проведём ось  и возьмем на ней произвольную точку
и возьмем на ней произвольную точку  . момент силы
. момент силы 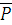 относительно центра будет изображаться вектором
относительно центра будет изображаться вектором 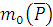 , перпендикулярным плоскости
, перпендикулярным плоскости  , причём по модулю
, причём по модулю
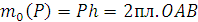 .
.
Проведём теперь через любую точку  плоскость
плоскость  , перпендикулярную оси
, перпендикулярную оси  ; проецируя силу
; проецируя силу 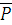 на эту плоскость, найдём:
на эту плоскость, найдём:

Но треугольник  представляет собой проекцию треугольника
представляет собой проекцию треугольника  на плоскость
на плоскость  . Угол между плоскостями треугольников равен
. Угол между плоскостями треугольников равен  .
.
Тогда  .
.
Умножим обе части уравнения на 2, находим

Так как произведение 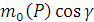 даёт проекцию
даёт проекцию  или
или  .
.
Момент силы 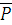 относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно центра, лежащего на этой оси. Или проекция вектора момента силы относительно центра на ось, проходящую через центр, равен моменту силы относительно этой оси.
относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно центра, лежащего на этой оси. Или проекция вектора момента силы относительно центра на ось, проходящую через центр, равен моменту силы относительно этой оси.
3.3.3. Главные векторы сил и моментов.
Главным вектором системы сил называется геометрическая сумма сил системы.

Рассмотрим систему сил, как угодно ориентированных в пространстве. Вычислим моменты этих сил относительно точки  .
.
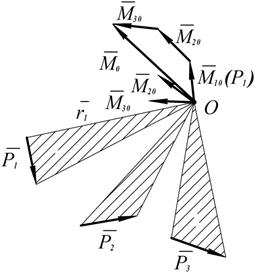
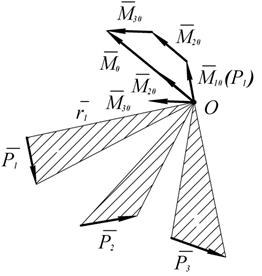

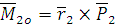

Векторы 
 все приложены в точке
все приложены в точке  . Построим многоугольник векторов моментов. Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра
. Построим многоугольник векторов моментов. Замыкающая сторона этого многоугольника – главный момент относительно неподвижного центра

Рис. 1.44 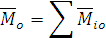
Таким образом, главным моментом пространственной системы сил относительно центра называется геометрическая сумма моментов сил системы относительно того же центра.
Главным моментом пространственной системы сил относительно неподвижной оси называется алгебраическая сумма моментов сил системы той же оси.

3.2.4. Приведение пространственной системы сил к заданному центру.
Приведение силы к заданному центру (метод Пуансо).
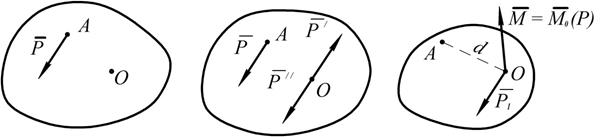
Рис. 1.45
Приведём силу к центру  . В точке
. В точке  приложим систему сил
приложим систему сил  , причём
, причём 
Силы  образуют пару, момент которой
образуют пару, момент которой 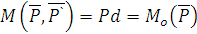 .
.
При приведении сил к заданному центру получаем в этом центре силу, геометрически равную заданной, и пару, момент которой равен моменту силы относительно центра приведения.
Теорема
При приведении пространственной системы сил к центру всегда получим силу, называемую главным вектором сил, приложенную в центре приведения и пару сил, момент которой равен главному моменту системы сил относительно центра приведения.
 Доказательство:
Доказательство:
Пусть имеем систему сил, как угодно ориентированных в пространстве (ограничимся тремя силами). Каждую силу приводим к центру  на основании метода Пуансо. В точке
на основании метода Пуансо. В точке  получим систему сходящихся сил
получим систему сходящихся сил  . Геометрическая сумма этих сил – есть главный вектор:
. Геометрическая сумма этих сил – есть главный вектор:  .
.
Векторы моментов

Рис. 1.46 так же образуют систему, сходящихся
векторов. Их геометрическая сумма – есть
главный момент системы сил
относительно центра 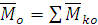 .
.
3.2.5. Вычисление главного вектора и главного момента пространственной системы сил.
Главный вектор:
 .
.
Спроектируем обе части этого векторного соотношения на оси 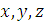 .
.

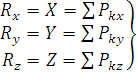
Тогда модуль 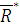 равен:
равен:

Направление 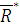 определяется направлением косинусов:
определяется направлением косинусов:
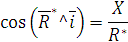
Рис. 1.47 

Главный момент
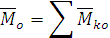
Спроектируем данное векторное соотношение на оси  :
:

Модуль главного момента равен
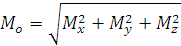
Направление определяем направлением косинусов:
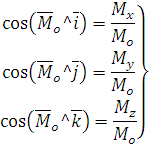
3.2.6. Условия и уравнения равновесия пространственной системы сил.
Теорема
Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю.
Доказательство:
Достаточность.
При  , система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при
, система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при 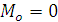 - система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
- система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
Необходимость. Пусть данная система сил эквивалентна нулю. Тогда необходимо, чтобы  .
.
Если какое-либо из этих условий не выполняется, то система сил приводится либо 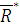 , либо к паре, момент которой
, либо к паре, момент которой  и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
Уравнения равновесия:


В случае произвольной пространственной системы сил задача является статически определенной, если число алгебраических неизвестных не более шести.
Дата добавления: 2015-06-17; просмотров: 1409;
