ЦЕНТР ТЯЖЕСТИ.
Сила тяжести – равнодействующая сил притяжения к Земле, она распределена
по всему объёму тела. Силы притяжения, приложенные к частицам твёрдого
тела, образуют систему сил, линии, действия которых сходятся в центре
Земли. Поскольку радиус Земли значительно больше размеров любого
земного тела, силы притяжения можно считать параллельными.
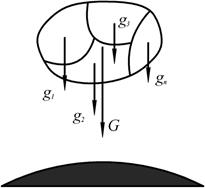
Рис. 1.48
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
Изображаем тело, составленное из нескольких частей  - силы тяжести частей, приложены в центрах тяжести частей.
- силы тяжести частей, приложены в центрах тяжести частей.
Пусть равнодействующая (сила тяжести всего тела) – приложена в неизвестном пока центре  .
.
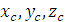 – координаты центра тяжести
– координаты центра тяжести  .
.
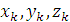 – координаты центров тяжести частей тела.
– координаты центров тяжести частей тела.
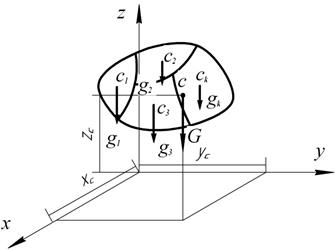
Рис. 1.49
Из теоремы Вариньона следует:
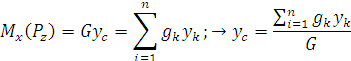
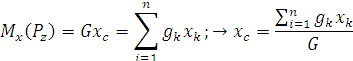

В однородном теле сила тяжести пропорциональна объёму  :
:
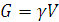 ,
,
 – вес единицы объёма
– вес единицы объёма
Следовательно, в формулах для однородных тел:
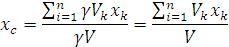

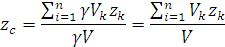
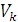 – объём элемента тела
– объём элемента тела
 – объём всего тела
– объём всего тела
Центр тяжести однородных плоских тел (плоских фигур).
Для плоских тел можно записать:
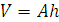 , где
, где  – площадь фигуры,
– площадь фигуры, 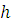 – её высота.
– её высота.
Тогда после подстановки в записанные выше формулы получим
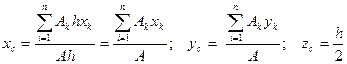
 – площадь части сечения
– площадь части сечения
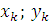 – координаты центра тяжести частей сечения
– координаты центра тяжести частей сечения
Выражение 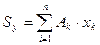 – называют статическим моментом площади
– называют статическим моментом площади 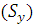 относительно оси y.
относительно оси y.
Аналогично 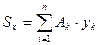 – статический момент относительно оси х.
– статический момент относительно оси х.
Тогда координаты центра тяжести сечения можно выразить:
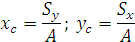
Оси, проходящие через центр тяжести, называются центральными. Статический момент относительно центральной оси равен нулю.
Положение центра тяжести простых геометрических фигур:
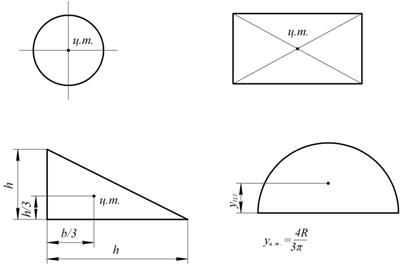
Рис.1.50
При решении задач необходимо учесть:
1. Центр тяжести симметричных фигур находятся на оси симметрии.
2. Сложные сечения разделяем на несколько простых.
3. Полости (отверстия)рассматриваются как часть сечения с отрицательной площадью.
Пример. Необходимо определить центр тяжести представленного сечения.
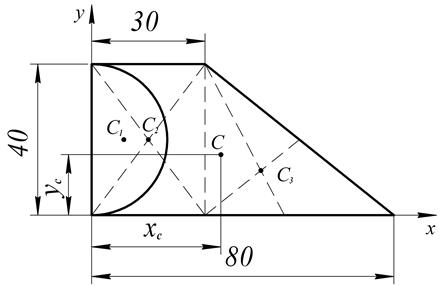
Рис.1.51
Разбиваем сечение на простейшие геометрические фигуры (прямоугольник, треугольник, половина круга).
Площадь прямоугольника

Площадь треугольника
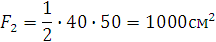
Площадь половины круга

Центр тяжести:
прямоугольника
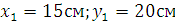
треугольника
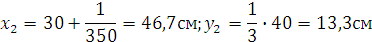
половины круга
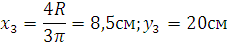
Положение центра тяжести, представленного сечения определяем по формуле
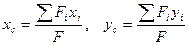 .
.
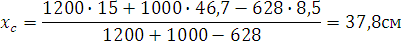
 .
.
Дата добавления: 2015-06-17; просмотров: 1284;
