Погрешности результата арифметических операций
Пусть дано несколько приближенных чисел, над которыми производятся арифметические операции – сложение, вычитание, умножение, деление. Если исходные числа приближенные, то результат арифметической операции также будет, вообще говоря, числом приближенным. Выясним, как связаны погрешности результата с погрешностями исходных чисел.
Пусть 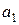 ,
, 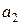 – приближенные числа для точных чисел
– приближенные числа для точных чисел 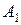 ,
, 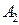 с соответственными предельными абсолютными погрешностями
с соответственными предельными абсолютными погрешностями 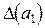 ,
, 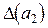 (
( 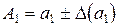 ,
, 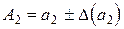 ). Найдем предельную абсолютную погрешность
). Найдем предельную абсолютную погрешность 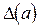 для суммы
для суммы 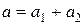 , являющейся приближением точной величины
, являющейся приближением точной величины 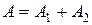 . По условию
. По условию 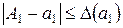 ,
, 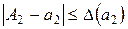 . Оцениваем истинную абсолютную погрешность числа
. Оцениваем истинную абсолютную погрешность числа 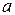 :
:
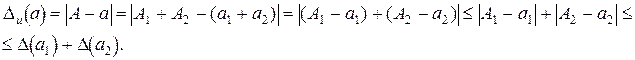
Итак, 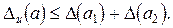 Исходя из определения предельной абсолютной погрешности следует, что в качестве
Исходя из определения предельной абсолютной погрешности следует, что в качестве 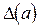 достаточно взять
достаточно взять 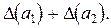
Аналогично рассуждая, можно установить, что 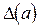 для разности
для разности 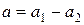 , являющейся приближением точной величины
, являющейся приближением точной величины 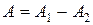 , также равна
, также равна 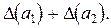
Итак, предельная абсолютная погрешность 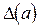 суммы
суммы 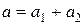 (разности
(разности 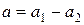 ) равна сумме предельных абсолютных погрешностей
) равна сумме предельных абсолютных погрешностей 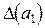 ,
, 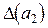
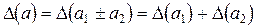 . (3.1)
. (3.1)
Формула (3.1) распространяется на любое конечное количество чисел.
Зная предельную абсолютную погрешность суммы (разности) двух чисел, можно найти предельную относительную погрешность их суммы (разности)
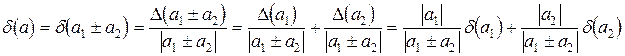 .
.
Пример 3.1. Пусть 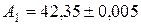 ,
, 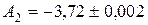 ,
, 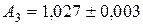 . Найти приближение
. Найти приближение 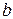 для точного числа
для точного числа 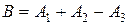 , вычислить погрешности. Результат округлить с сохранением верных цифр.
, вычислить погрешности. Результат округлить с сохранением верных цифр.
Решение:1) По условию имеем: 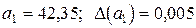 ;
; 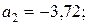
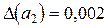 ;
; 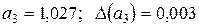 . Тогда приближенное число
. Тогда приближенное число
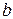 =
= 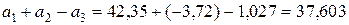 .
.
2) Вычисляем предельные абсолютную и относительную погрешности, пользуясь равенством (3.1)
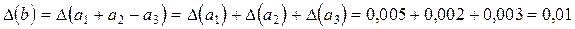 ;
;
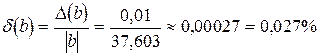 .
.
3) Итак, 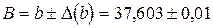 . Так как
. Так как 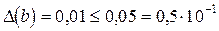 , то в приближенном числе
, то в приближенном числе 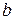 =37,603 верными будут первые три цифры:
=37,603 верными будут первые три цифры: 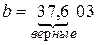 . Округляя результат до верных цифр (то есть до десятых), получим
. Округляя результат до верных цифр (то есть до десятых), получим 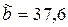 .
.
4) Погрешность
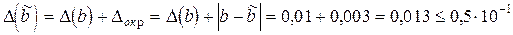 ,
,
как видно, не изменила количество верных цифр в числе 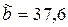 .
.
Ответ: 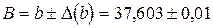 ;
; 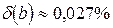 ;
; 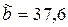 .
.
Рассмотрим теперь операцию умножения (будем использовать введенные выше обозначения 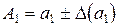 ,
, 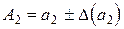 ). Найдем предельную относительную погрешность
). Найдем предельную относительную погрешность 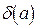 для произведения
для произведения 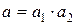 , являющегося приближением точной величины
, являющегося приближением точной величины 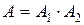 . Оценим сначала истинную абсолютную погрешность числа
. Оценим сначала истинную абсолютную погрешность числа 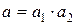
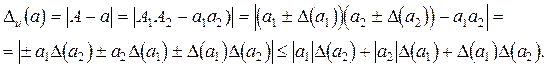
Оценим истинную относительную погрешность числа 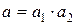
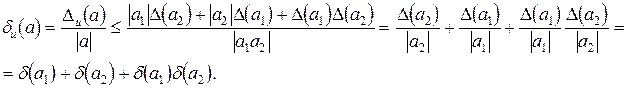
Итак, 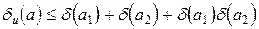 . Так как
. Так как 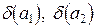 – малы, то слагаемым
– малы, то слагаемым 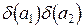 можно пренебречь по сравнению с
можно пренебречь по сравнению с 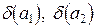 . А тогда по определению предельной относительной погрешности в качестве
. А тогда по определению предельной относительной погрешности в качестве 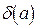 достаточно взять
достаточно взять 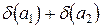 , то есть:
, то есть:
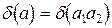 =
= 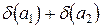 . (3.2)
. (3.2)
Предельная относительная погрешность 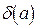 частного
частного 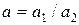 (
( 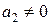 ), являющегося приближением точной величины
), являющегося приближением точной величины 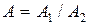 , равна
, равна
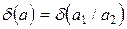 =
= 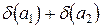 . (3.3)
. (3.3)
Итак, предельная относительная погрешность 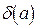 произведения
произведения 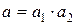 (частного
(частного 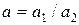 ) равна сумме предельных относительных погрешностей
) равна сумме предельных относительных погрешностей 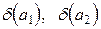 .
.
Найдя 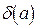 , можно вычислить
, можно вычислить 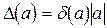 . Общая формула в этом случае будет иметь вид
. Общая формула в этом случае будет иметь вид
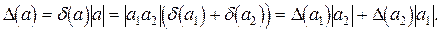
Формулы (3.2), (3.3) распространяются на любое конечное количество чисел. В частности, нетрудно установить, что
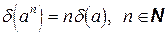 . (3.4)
. (3.4)
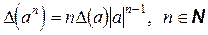 . (3.5)
. (3.5)
Докажем, например, формулу (3.5). Имеем (применяем формулу (3.4))
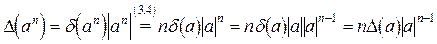 .
.
При вычислении погрешностей 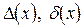 числа
числа 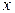 – результата арифметических операций необходимо проверить, какое из арифметических действий выполняется последним. Если последнее действие сложение или вычитание, то необходимо сначала вычислить
– результата арифметических операций необходимо проверить, какое из арифметических действий выполняется последним. Если последнее действие сложение или вычитание, то необходимо сначала вычислить 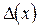 (пользуясь (3.1)). Если последнее действие умножение или деление, то сначала вычисляют
(пользуясь (3.1)). Если последнее действие умножение или деление, то сначала вычисляют 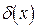 (пользуясь (3.2) или (3.3)). При нахождении погрешностей промежуточных вычислений пользуются таким же правилом.
(пользуясь (3.2) или (3.3)). При нахождении погрешностей промежуточных вычислений пользуются таким же правилом.
Пример 3.2. Найти для 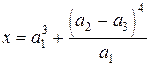 погрешности
погрешности 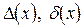 (предполагать, что известны числовые значения для
(предполагать, что известны числовые значения для 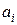 ,
, 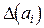
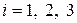 ).
).
Решение: В данном случае последней операцией является операция сложения. Поэтому сначала применяем формулу (3.1) для нахождения 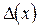 :
:
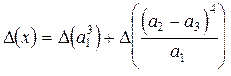 .
.
Теперь находим по отдельности предельные абсолютные погрешности.
a) 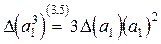 (применили формулу (3.5));
(применили формулу (3.5));
б) 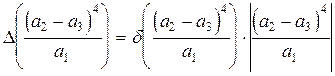 (воспользовались определением предельной относительной погрешности, формула (1.6)),
(воспользовались определением предельной относительной погрешности, формула (1.6)),
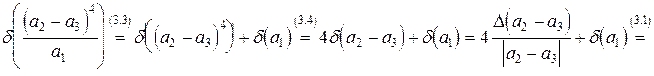
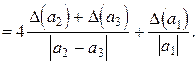
Итак, 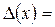
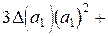
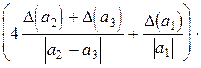
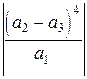 ,
, 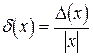 .
.
Пример 3.3. Пусть числа 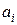 ,
, 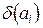 – известны (
– известны ( 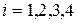 ). Выразить для числа
). Выразить для числа 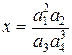 погрешность
погрешность 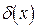 через погрешности
через погрешности 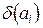 (
( 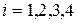 ).
).
Решение: Обозначим 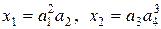 ,
, 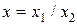 . Последней операцией является операция деления. Тогда, используя последовательно формулы (3.3), (3.2), (3.4), получим
. Последней операцией является операция деления. Тогда, используя последовательно формулы (3.3), (3.2), (3.4), получим
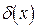 =
= 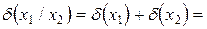
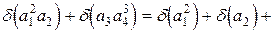
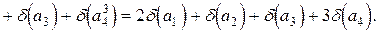
Пример 3.4. Пусть 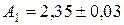 ,
, 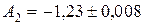 ,
, 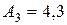 ,
,
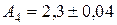 . Вычислить
. Вычислить 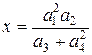 ,
, 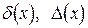 . Результат округлить с
. Результат округлить с
сохранением верных цифр.
Решение:
1) По условию имеем 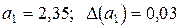 ;
; 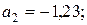
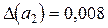 ;
; 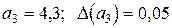 ;
; 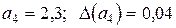 . Вычисляем сначала число
. Вычисляем сначала число
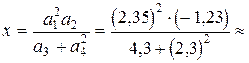 –0,7083.
–0,7083.
2) Пользуясь формулами (3.1)–(3.4), найдем выражение для 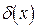 через известные числа
через известные числа 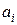 (
( 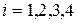 ) и предельные абсолютные погрешности
) и предельные абсолютные погрешности 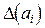 :
:
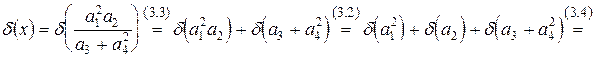
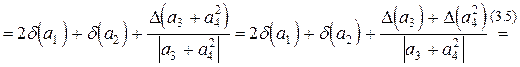
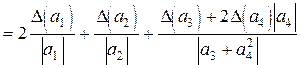 .
.
Теперь в полученное выражение для 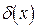 подставляем исходные данные. Получаем
подставляем исходные данные. Получаем 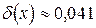 . Тогда
. Тогда 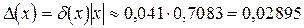 . Итак, получаем
. Итак, получаем 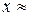 –0,7083,
–0,7083, 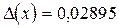 .
.
3) Так как 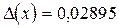
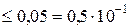 , то в числе
, то в числе 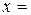 –0,7083 верными являются первые две цифры:
–0,7083 верными являются первые две цифры: 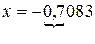 . Округляем результат, сохраняя верные цифры (до десятых):
. Округляем результат, сохраняя верные цифры (до десятых): 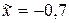 . Погрешность округленного числа равна
. Погрешность округленного числа равна
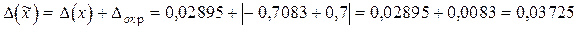 .
.
Видно, что в округленном числе 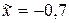 все цифре верные, так как
все цифре верные, так как 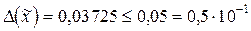 .
.
Ответ: 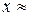 –0,7083;
–0,7083; 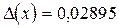 ;
; 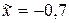 .
.
Дата добавления: 2015-04-25; просмотров: 7419;
