Анализ доходности и риска финансовых операций на основе принципа оптимальности Парето
Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку, цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками.
Обычно финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль, так и убыток (или незначительная прибыль по сравнению с ожидаемой).
Существует несколько способов оценки финансовой операции с точки зрения ее доходности и риска. Наиболее часто доход операции представляется случайной величиной Q, а риск операции r оценивается средним квадратическим отклонением этого случайного дохода.
Постановка задачи в общем виде. Пусть А – некоторое множество операций, которые различаются хотя бы одной характеристикой. При выборе наилучшей операции желательно, чтобы Q было больше, а r меньше.
Считают, что операция а доминирует операцию b (обозначается а > b), если Q (а) ≥ Q (b) и r(a) ≤ r(b) и хотя бы одно из этих неравенств строгое. При этом операция а называется доминирующей, а операция b – доминируемой. Причем никакая доминируемая операция не может быть признана наилучшей, поэтому наилучшую операцию следует искать среди недоминируемых операций. Множество недоминируемых операций называется множеством (областью) Парето или множеством оптимальности по Парето[4].
Для множества Парето справедливо утверждение: каждая из характеристик Q, r является однозначной функцией другой, т.е. на множестве Парето по одной характеристике операции можно однозначно определить другую.
Пример. 3.8. Из четырех возможных финансовых операций с ожидаемыми доходностями Q1, Q2, Q3, Q4 и соответствующими вероятностями их получения p1, p2, p3 , p4 необходимо выбрать операцию оптимальную по Парето.
Значения ожидаемых доходностей qj и соответствующих им вероятностей pj приведены в следующей матрице
p1 p2 p3 p4
1/2 1/6 1/6 1/6
Q1 1 2 3 5
Q2 2 0 5 8
Q3 3 4 5 8
Q4 3 3 6 7 .
Решение
Поскольку ожидаемый доход финансовой операции считается случайной величиной Q, то его среднее значение оценивают математическим ожиданием: 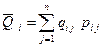 , (3.16)
, (3.16)
где pi j - вероятность получения дохода qi j в i – ой финансовой операции.
Количественной мерой риска r финансовой операции считается s - среднее квадратическое отклонение
r i = 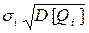 , (3.17)
, (3.17)
которое характеризует степень разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Дисперсию доходности D[Qi] удобно оценивать по формуле: D[Q i] = M [(Q i - 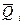 ) 2 ] = M [Q i 2 ] – [
) 2 ] = M [Q i 2 ] – [ 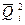 ] .
] .
Здесь M [Q i 2 ] = å q 2i j pi j – математическое ожидание квадрата ожидаемой доходности в i-ой финансовой операции.
Расчеты средних ожидаемых доходов и рисков по вышеприведенным формулам выполним в среде Excel. Рабочий лист с исходными данными, расчетными формулами и результатами расчета средних доходностей Q c p и риска r приведен на рис. 3.14.
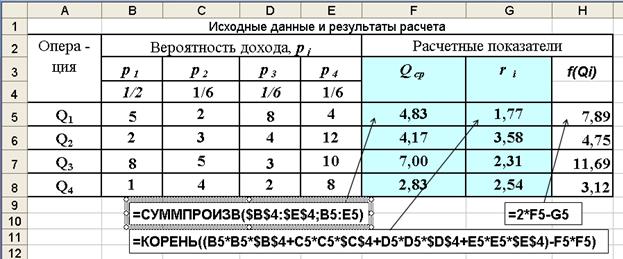
Рис. 3.14. Общий вид рабочего листа с результатами расчета
Найденные в результате расчета средние ожидаемые доходы`Qi и соответствующие им риски ri нанесем на график в системе координат: доход (вертикальная ось) - риски (горизонтальная ось), рис. 3.15.
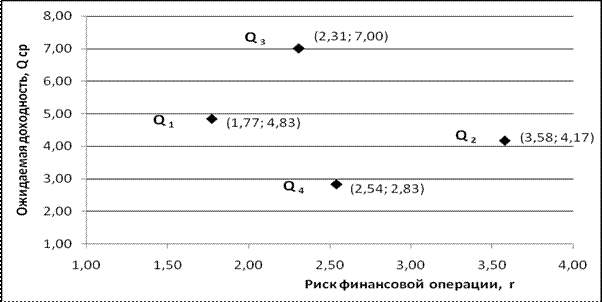
Рис. 3.15. Графическая интерпретация результатов расчета эффективности финансовых операций в системе координат: ожидаемая доходность – риск
Проанализируем взаимное расположение 4-х точек на графике с позиции их доминирования. Чем выше точка (`Q, r), тем более доходная операция, чем точка правее - тем операция более рисковая. Значит, нужно выбирать точку выше и левее. Точка (`Q¢, r¢) доминирует точку (`Q, r) если `Q¢ ³`Q и r¢ £ r. В данном случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы - доходность 3-й больше, но и риск ее тоже больше.
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Выбор лучшей из рассматриваемых операций производится обязательно из операций, оптимальных по Парето.
Для нахождения лучшей операции иногда применяют взвешивающую формулу, которая для пар (`Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула имеет вид:
j(`Q ) = 2×`Q - r . Тогда получаем: j(`Q 1) = 2*4,83 -1,77 = 7,89; j(`Q 2) = 4,75; j(`Q 3)= 11,69; j(`Q 4)= 3,12.
На рис. 3.16. приведена графическая иллюстрация результатов, полученных с помощью взвешивающей формулы.
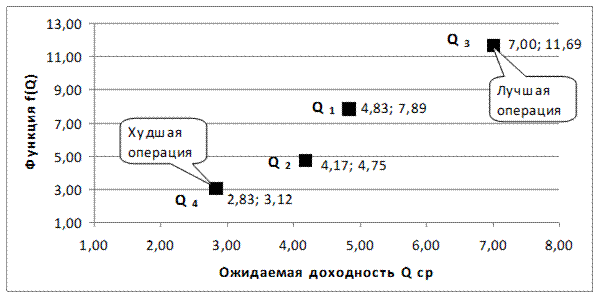
Рис.3.16. Множество операций
Из последнего рисунка видно, что 3-я операция – лучшая, расположена в правом верхнем углу графика, а 4-я – худшая занимает левый нижний угол.
3.6. Экспертные методы оценки риска
Когда из-за отсутствия данных, нельзя использовать количественные методы прогнозирования показателей риска, могут использоваться экспертные методы оценки риска. Задача экспертного оценивания сводится к получению группового субъективного мнения на основе обработки совокупности индивидуальных мнений экспертов.
Методы экспертной оценки риска – совокупность логических и математических процедур позволяющих получать информацию от специалистов-экспертов, проводить ее анализ и обобщать результаты для выбора рациональных решений.
Среди методов экспертных оценок выделяются две группы: коллективные методы оценивания и методы получения индивидуального мнения экспертов.
Коллективные методы оценивания («мозговая атака», деловые игры, сценарии, совещания, «суд») предполагают выработку общего мнения в ходе совместного обсуждения.
Методы получения индивидуального мнения (анкетный опрос, Дельфи, интервью) построены на предварительном сборе информации от опрашиваемых индивидуально экспертов.
Применение экспертных методов оценки риска связано с реализацией следующих этапов:
- определение цели и задач экспертного оценивания;
- формирование рабочей группы для управления и проведения экспертного оценивания;
- выбор метода получения экспертной информации и способов ее обработки;
- формирование группы экспертов и разработка анкет опроса;
- опрос экспертов (проведение экспертизы);
- обработка и анализ результатов экспертизы;
- интерпретация полученных результатов;
- составление отчета.
На первом этапе определения цели экспертизы устанавливается признак, по которому производится оценка. Если целей несколько, то оценки по различным шкалам целесообразно свести к единой шкале, например за счет установления цели более высокого уровня.
Методы групповой экспертной оценки делятся на два вида: открытая дискуссия и анкетный опрос.
Метод открытой дискуссии имеет ряд недостатков: не исключается давление авторитетов, затруднена математическая обработка обобщенного мнения группы экспертов и степени их согласованности.
Опрос экспертов с помощью анкет устраняет недостатки методов открытой дискуссии, поскольку свои заключения по поставленным вопросам эксперты представляют анонимно.
Формирование группы экспертов связано с вопросами определения ее качественного и количественного состава.
При качественном отборе к экспертам предъявляются следующие требования: информированность, высокий уровень общей эрудиции, отсутствие личной заинтересованности в результатах экспертизы, глубокие специальные знания в оцениваемой области деловитость и объективность, наличие производственного и (или) исследовательского опыта в данной области и т.д.
Степень компетентности экспертов оценивается одним из двух способов: объективный способ; субъективный способ.
Наиболее часто пользуются субъективными способами, которые в свою очередь делятся на два вида:
взаимооценочные – уровень компетентности экспертов определяется по характеристикам, данных им другими участниками экспертизы;
самооценочные – сам эксперт определяет вес своей оценки по некоторому вопросу, пользуясь оценочной шкалой, представляемой ему прогнозистом.
Второй способ определения компетентности экспертов более простой с точки зрения получения исходных данных, поскольку не требует предварительной обработки данных для получения веса оценки эксперта.
Компетентность эксперта (К) оценивается степенью его квалификации, которая определяется на основе суждений эксперта о своей информированности по решаемой проблеме (Ки) и уровне аргументации своих мнений (Ка): К = 0,5 (Ки + Ка).
Увеличение количества экспертов приводит к снижению погрешности экспертной оценки, но при этом точность прогноза растет медленнее количества экспертов. На практике подбирается компромиссный вариант между требуемой точностью и стоимостью прогноза. Считается, что в состав группы целесообразно включать не менее 5-12 специалистов.
На точность групповых оценок также влияет и степень согласованности ответов экспертов.
Вопросы для экспертов, могут иметь содержательный ответ в развернутой форме или в виде количественной оценки.
В последнем случае возможно применение математических методов обработки результатов.
Метод «Дельфи» реализует анкетный способ опроса при прогнозировании количественных показателей. Для повышения достоверности групповой оценки экспертиза проводится в 3-4 тура. После каждого тура экспертов знакомят с результатами прежнего тура перед началом следующего.
Доверительная вероятность такого прогноза составляет 50%.
3.5.1. Метод «Дельфи»
Рассмотрим алгоритм обработки результатов методом «Дельфи» на конкретном примере.
Пример. 3.9. Десять экспертов оценили прогнозные значения экономического показателя Y. Найти методом «Дельфи» точечный и интервальный прогнозы.
| Наименование | Эксперт, j | |||||||||
| Показатель, x | 16,9 | 13,8 | 11,9 | 12,3 | 16,3 | 16,1 | 20,6 | 16,8 | 13,1 |
Решение
Алгоритм обработки результатов методом «Дельфи» содержит следующие этапы.
1. Результаты оценок экспертов ранжируются в порядке возрастания.
| 11,9 | 12,0 | 12,3 | 13,1 | 13,8 | 16,1 | 16,3 | 16,8 | 16,9 | 20,6 |
2. Определяется количество интервалов (N) между первым и последним значениями ранжированного ряда. Для данных условий между первым и последним значением ряда находится 9 интервалов.
3. Рассчитывается количество интервалов приходящихся на один (N/4), два (N/2) и три (ЗN/4) квартиля, соответственно: на один квартиль: 9/4 = 2,25 интервала, на два квартиля - 4,5 и на три 6,75 интервалов, соответственно.
4. Для нахождения первого квартиля Q1 смещаемся от первого члена ряда на 2 интервала и получаем значение 12,3. к этому значению надо добавить число, равное произведению 0,25 на разность (13,1-12,3). Таким образом, имеем
нижняя граница доверительного интервала будет равна:

точечный прогноз показателя:

верхняя граница доверительного интервала:

Дата добавления: 2015-05-28; просмотров: 3740;
