Основные характеристики портфеля ценных бумаг
Если предприятие располагает достаточным резервом финансовых средств, то оно само может стать инвестором, т.е. вкладывая финансовые средства в ценные бумаги других организаций, оно может получать дополнительную прибыль. Процесс инвестирования характеризуется временем, доходностью и риском. Вложив финансовые средства сейчас, возможное вознаграждение наступает позже и его величина обычно заранее неизвестна.
Такие операции связаны с формированием инвестиционных портфелей, оценка эффективности которых производится по показателям доходности и риска. В связи с этим рассмотрим основы формирования и управления такими портфелями и методы оценки их эффективности. Управление инвестициями представляет собой управление денежными средствами.
Различают реальные и финансовые инвестиции. Реальные инвестиции обычно включают инвестиции в материально осязаемые активы (земля, оборудование, заводы и пр. активы), а финансовые инвестиции представляют собой контракты, оформленные на бумаге (акции облигации и пр.).
Процесс управления инвестициями обычно включает пять этапов:
1) формулирование инвестиционных целей,
2) формирование инвестиционной политики для достижения выбранных целей,
3) выбор портфельной стратегии с учетом выбранных инвестиционных целей и политики,
4) выбор активов, которые предстоит включить в состав портфеля,
5) измерение и оценка эффективности инвестиций.
Портфель – это совокупность инвестиций в ценные бумаги, обращающихся на финансовом рынке, обеспечивающая достижение инвестиционной цели вкладчика. В состав портфеля могут включаться бумаги только одного типа (акции или облигации) или различного типа (акции, облигации, депозитные и сберегательные сертификаты и т. д.).
Портфельный менеджмент рассматривает принципы формирования инвестиционного портфеля ценных бумаг. Методология инвестиционного менеджмента начала складываться в двадцатые годы прошлого столетия с появлением понятия <истинной> цены (fair price) акции. Задача инвестора состоит в приобретении недооцененных ценных бумаг, рыночная цена которых на момент покупки ниже истинной, и избавлении от переоцененных бумаг, тем самым в перспективе инвестор получает прибыль.
Основы теории финансового портфеля были заложены в статье Гарри Марковица «Выбор портфеля» (1952), в которой он предложил математическую модель формирования оптимального портфеля ценных бумаг и методы построения таких портфелей при определенных условиях. Такая оптимизационная задача относится к классу задач квадратической оптимизации при линейных ограничениях. К настоящему времени подобные оптимизационные задачи вместе с задачами линейного программирования имеют эффективные алгоритмы их решения, в том числе в среде Excel.
Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965) были введены понятия систематического (рыночного) и несистематического рисков ценной бумаги.
Риск (общий риск) ценной бумаги состоит в неопределенности ее дохода на конец периода инвестирования. Количественно риск измеряется дисперсией доходности ценной бумаги за определенный интервал времени, например, месяц, квартал, год и т. д.
Систематический или рыночный риск акции - это та часть общего риска, которая зависит от факторов, общих для всего рынка ценных бумаг. К ним относятся неожиданные изменения макроэкономических показателей (ВВП, скорость промышленного роста, собираемость налогов, процентная ставка, уровень инфляции и т. д.), изменение политической ситуации в стране или в мире, психологический настрой участников рынка и др.
Несистематический, или собственный риск - это часть общего риска, зависящая только от состояния дел в данной компании, которое характеризуется неожиданными изменениями таких факторов, как вероятность смены руководства, наличие долгосрочных договоров, просроченной дебиторской или кредиторской задолженности, показатели финансового состояния и др.
Математически разделение рисков обычно проводится с помощью уравнения линейной регрессии, связывающего доходность акции с доходностью по рыночному индексу.
Коэффициент регрессии называется коэффициентом бета ценной бумаги и является характеристикой ее рыночного риска. В качестве рыночного обычно берется индекс, достаточно полно отражающий состояние дел в экономике в целом и включающий курсы акций крупных компаний в различных секторах рынка. Обычно за основу расчета индекса берется капитализация входящих в него ценных бумаг.
Общий риск ценной бумаги может представляться не только в виде суммы собственного и несобственного рисков, но и в виде суммы трех слагаемых, где в качестве третьей компоненты выступает риск отрасли, к которой относится компания или в виде многофакторных моделей.
Главная цель в формировании портфеля для инвестора - достижение оптимального сочетания между риском и доходом, т. е. набор инвестиционных инструментов призван снизить до минимума риск его потерь и одновременно максимизировать его доход.
Для получения количественных характеристик инвестиционного портфеля могут использоваться следующие показатели:
1. Доходность портфеля (mp) ценных бумаг - взвешенная средняя из ожидаемых доходов по каждому из компонентов
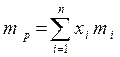 (4.1.)
(4.1.)
где xi - доли инвестиций (портфельные веса), помещенных в каждый из видов активов записываются в виде вектора XT = (х1, х2, … хn);
mi - ожидаемая ставка дохода по каждому виду активов.
2. риск портфеля -sp - стандартное отклонение ставок дохода по портфелю, рассчитывается как квадратный корень из дисперсии портфельного дохода (вариации Vp), которая определяется по формуле:
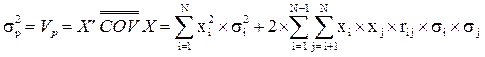 , (4.2.)
, (4.2.)
где 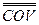 -ковариационная матрица порядка N.
-ковариационная матрица порядка N.
Ковариация - это статистическая мера взаимодействия двух случайных переменных, например, доходности двух ценных бумаг.
Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют однонаправленную тенденцию изменения. Ковариация будет низкой, если колебания доходности двух активов носят случайный характер, либо колеблемость одного из них невелика. Ковариация между двумя акциями x и y рассчитывается следующим образом:
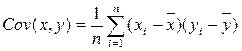 . (4.3)
. (4.3)
Поскольку содержательная интерпретация численного значения ковариации достаточно сложна, то для измерения силы связи между двумя переменными чаще используется коэффициент корреляции. Этот коэффициент стандартизирует ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и позволяет привести величины к сопоставимому виду.
Коэффициент корреляции между двумя переменными i и j можно рассчитать по выражению:
r i,j = 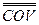 i, j / s i ´s j ,(4.4)
i, j / s i ´s j ,(4.4)
Знак коэффициента корреляции совпадает со знаком ковариации. Его положительные значения соответствуют изменению переменных в одном направлении, а отрицательные – в противоположных направлениях. Если значение r i,jблизко к нулю, то связь между переменными слабая. Коэффициент корреляции изменяется в интервале от – 1,0 до +1,0.
В реальных условиях могут проявляться частные случаи:
1) совершенная положительная корреляция (рис. 4.1.а), например, при приобретении двух видов обычных акций одной корпорации, выпущенных на одинаковых условиях, когда одна из двух ценных бумаг имеет относительно высокую доходность, то и другая ценная бумага так же будет иметь относительно высокую доходность. В этом случае стандартное отклонение ставок дохода по портфелю рассчитывается как средневзвешенная из стандартных отклонений доходов, входящих в состав портфеля активов.

Рис. 4.1. Варианты взаимосвязи доходностей двух ценных бумаг A и B
2) совершенная отрицательная корреляция (рис. 4.1.б) проявляется в том, что с уменьшением дохода на один пункт по одной акции происходит увеличение дохода на один пункт по другой акции и наоборот. В этом случае инвестор может уменьшить стандартное отклонение дохода по этим двум активам вместе до нуля, т.е. свести риск к минимуму.
3) отсутствие коррелированной доходности (рис. 4.1.в) означает, что невозможно установить взаимосвязь между ценными бумагами.
Последняя формула может использоваться для расчета ковариации:
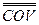 i, j = ri, j ´s i ´s j , (4.5)
i, j = ri, j ´s i ´s j , (4.5)
гдеs i , s j – стандартные отклонения доходов по i-му и j-му активам, соответственно,
ri j – коэффициент корреляции доходов между i-м и j-м активами.
Дата добавления: 2015-05-28; просмотров: 2230;
