Постановка задачи об оптимальном портфеле
В литературе описаны различные подходы к формированию оптимального портфеля с помощью моделей Блэка, Марковица, Тобина.
Задача оптимизации сводится к определению такой структуры состава портфеля инвестиций, чтобы величина ожидаемого дохода и уровень риска соответствовали целям инвесторов. При этом целевой функцией может быть минимизация риска при заданной доходности, либо максимизация дохода при риске не выше заданного. На компоненты вектора Х, представляющего состав портфеля могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д. Портфели, удовлетворяющие условиям данного рынка, называются допустимыми.
1) В модели Блэка допустимыми являются любые портфели, т.е. вектор Х удовлетворяет лишь основному ограничению:
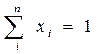 . (4.6)
. (4.6)
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно за счет большого риска.
2) Модель Марковица рассматривает в качестве допустимых только стандартные портфели (без коротких позиций). Это значит, что на вектор Х накладываются два ограничения: основное 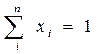 и неотрицательности xi ³ 0 для всех i.
и неотрицательности xi ³ 0 для всех i.
Портфель называют стандартным, если инвестор по каждому активу находится в длинной (long) позиции.
Длинная позиция - это обычно покупка актива с намерением его последующей продажи (закрытие позиций). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи. Если относительно некоторого актива инвестор уверен в обратном, то есть в понижении его стоимости, то он может совершить сделку, которая называется «короткой продажей» (short sale). Для этого он берет данный актив взаймы у другого инвестора (кредитора), сразу же продает его, а впоследствии покупает на рынке по сниженной цене и возвращает его своему кредитору. При этом он обязан выплатить кредитору текущий доход по активу за время сделки и некоторый процент за предоставление самой возможности сделки (за кредит). На большинстве фондовых бирж короткие продажи вполне допустимы и часто используются, но ввиду их особой рискованности биржи могут вводить ограничения на общую величину коротких позиций в сделках.
В модели Марковица обычно рассматриваются два типа задач оптимизации портфелей: минимального риска при заданном уровне доходности, и максимальной эффективности при уровне риска не превышающем заданного значения.
Портфель Марковица минимального риска. Постановку данной задачи можно интерпретировать следующим образом. Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
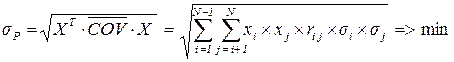 (4.7)
(4.7)
при заданной эффективности портфеля
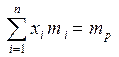 , (4.8)
, (4.8)
и условии, что сумма долей активов в портфеле должна составлять единицу
S xi = 1,0. (4.9)
Здесь матрица ковариаций 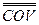 i j =
i j = 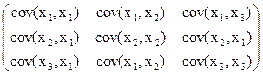 .
.
Пример 4.2. Сформировать портфель минимального риска sp из двух видов ценных бумаг А с эффективностью 12% и риском 21,2 и В с эффективностью 5,1% и риском 8,3 при условии, что обеспечивается доходность портфеля (mp =S xi mi) не менее 8,9%. Коэффициент парной корреляции между этими бумагами равен 0,18.
Решение
1. Введем обозначения: x1 - доля в портфеле ценных бумаг А; x2 - доля в портфеле ценных бумаг В,
2. Сформулируем задачу формирования оптимального портфеля по модели Марковица, с учетом исходных данных.
Необходимо найти вектор Х* = (x1, x2), минимизирующий риск портфеля:
sp=  =
= 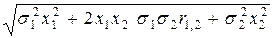 =
=
= 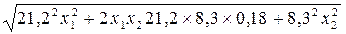 ® min,
® min,
при следующих ограничениях:
- по доходности 12´ x 1 + 5,1´ x 2³ 8,9;
- по составу портфеля x 1 + x 2 =1;
- условие неотрицательности x 1, x 2 ³ 0.
Данная задача свелась к задаче квадратического программирования.
3. Решение приведенной задачи можно осуществить графическим методом, либо используя надстройку в Excel Поиск решения.
Графическая иллюстрация решения задачи представлена на рис. 4.5.
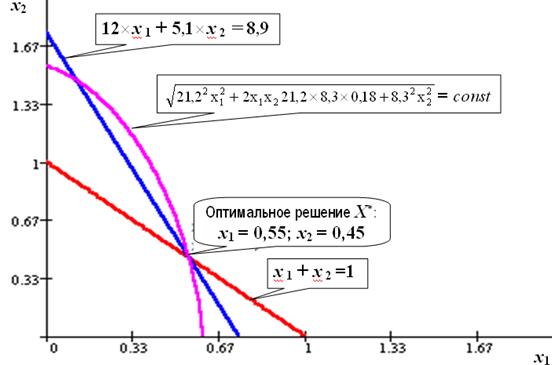
Рис. 4.5. Минимальный риск портфеля равный 12,88 достигается в точке пересечения трех линий (x 1=0,55 и x 2=0,45), соответствующих ограничениям 12´ x 1 + 5,1´ x 2³8,9 и x1 + x 2 =1 и целевой функции
Для решения с помощью надстройки Поиск решения вначале на листе Excel составляется стандартная форма для решения оптимизационных задач, с использованием надстройки Поиск решения как показано на рис. 4.6. Затем непосредственно используется сама надстройка Поиск решения.
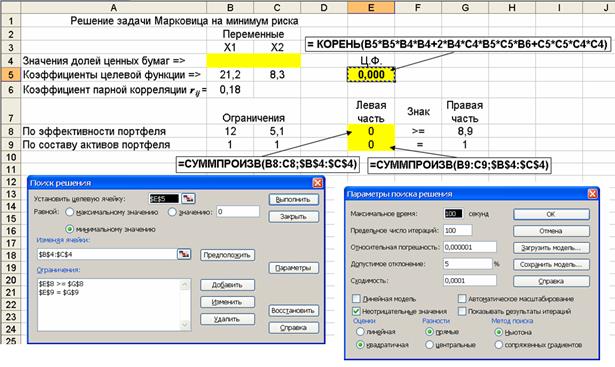
Рис. 4.6. Исходные данные и расчетные формулы
Результаты расчета состава оптимального портфеля по критерию минимального риска представлены на рис. 4.7.
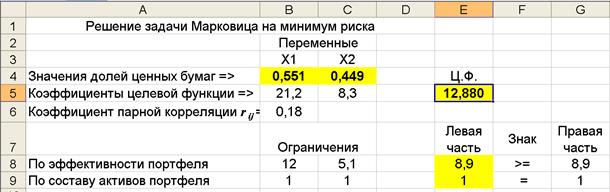
Рис.4.7. Результаты расчета состава оптимального портфеля
В ячейке Е5 получено минимальное значение целевой функции σp = 12,880, а в ячейки B4:C4 записаны значения x1 = 0,551 и x2 = 0,449 - доли ценных бумаг типа A и типа B, соответственно. При этом заданные ограничения удовлетворяются полностью, эффективность портфеля составляет 8,9% (ячейка G8).
Пример 4.3. Сформировать портфель минимального риска из трех ценных бумаг А, В и С (характеристики бумаг приведены в таблице), обеспечиваю-
| Показатель | Тип ценной бумаги | ||
| A | B | C | |
| Эффективность, mi , % | 5,1 | 9,5 | |
| Риск, σi | 21,2 | 8,3 | 14,5 |
щих среднюю доходность портфеля mp не менее 12,5%. Матрица коэффициентов парной корреляции между ценными бумагами известна:
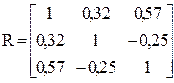
Решение
1. Введем обозначения: x1, x2, x3 – соответствующие доли ценных бумаг А, В и С в составе портфеля.
2. Запишем экономико-математическую модель (ЭММ) задачи формирования оптимального портфеля по модели Марковица в общем виде:
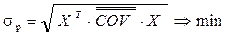 ,
,
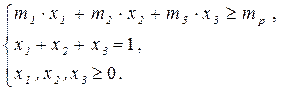
3. Подготовим лист для решения задачи, рис. 4.8. и здесь же предварительно сформируем ковариационную матрицу (ячейки F17:H19), элементы которой рассчитываются по выражению (4.5).
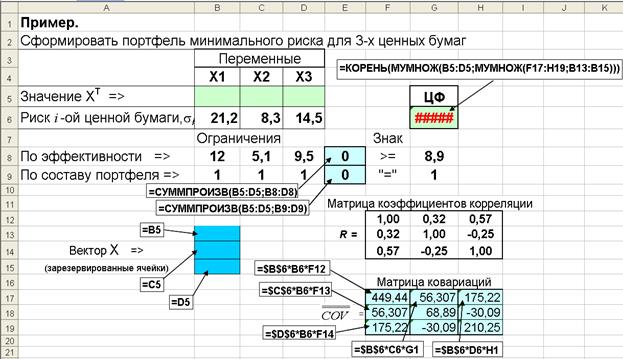
Рис. 4.8. Лист Excel с исходными данными и расчетными формулами для расчета состава оптимального портфеля из трех ценных бумаг
4. Запишем ЭММ задачи в развернутом виде с учетом исходных условий и рассчитанной матрицы ковариаций:
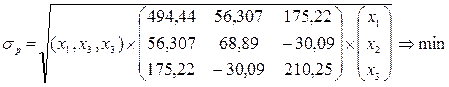

5. В результате решения задачи в ячейках (B5:D5) будут находиться элементы оптимального вектора Х* = (0,23; 0,27; 0,50), минимизирующего риск портфеля, который составляет σp = 1,01 (ячейка G6) и обеспечивающий его эффективность 8,9% (ячейка E8), рис.4.9.

Рис. 4.9. Лист Excel с результатами расчета состава оптимального портфеля из трех ценных бумаг
Портфель Марковица максимальной эффективности. Найти вектор X*, максимизирующий ожидаемую эффективность портфеля
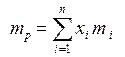 => max (4.10)
=> max (4.10)
при уровне риска не превышающем заданного значения
 , (4.11)
, (4.11)
и условии, что сумма долей активов в портфеле должна составлять единицу
S xi = 1,0. (4.12)
Если в оптимальном решении значения xi* ³ 0, то рекомендуется долю xi* наличного капитала вложить в ценные бумаги i-го вида. Если xi* < 0, то следует провести операцию «короткой продажи» и если такая операция невозможна, то необходимо в модель ввести ограничение xi* ³ 0. Вместо операции «короткой продажи» инвестор может воспользоваться денежными средствами по безрисковой ставке.
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.
Пример 4.4.Найти оптимальный портфель максимальной эффективности для трех ценных бумаг R, S и L с известными доходностями mi и риском σi (см. табл.):
| R | S | L | |
| mi (%) | 10,5 | ||
| si |
Коэффициенты парной корреляции между ценными бумагами представлены в виде матрицы:
| R | S | L | |
| R | 0,52 | 0,27 | |
| S | 0,52 | 0,75 | |
| L | 0,27 | 0,75 |
Верхняя граница риска σp не должна превышать 16.
Решение
1. Введем обозначения: x1, x2, x3 – соответствующие доли ценных бумаг типов R, S и L в составе портфеля.
2. Запишем ЭММ задачи формирования оптимального портфеля по модели Марковица в общем виде:
mp= m1´ x1+ m2´ x2+ m3´ x3 => max ,
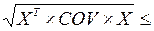 σp ,
σp ,
S x i = 1,0 .
3. Сформулируем ЭММ задачи с учетом конкретных исходных данных. Найти вектор Х= (x1, x 2, x 3), максимизирующий доходность портфеля mp.
mp=12´ x 1+10,5´ x 2+11´ x 3 => max
при следующих ограничениях
sp = 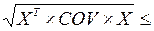 16
16
x 1 + x 2 + x 3 =1
x 1, x 2, x 3 ³ 0
Здесь матрица ковариаций так же получена с использованием формулы (4.5) COVi,j= ri,j ´ si ´ sj,
COV= 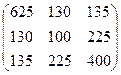

Для решения задачи используется надстройка EXCEL Поиск решения. Исходные данные и расчетные формулы представлены на рис. 4.10.
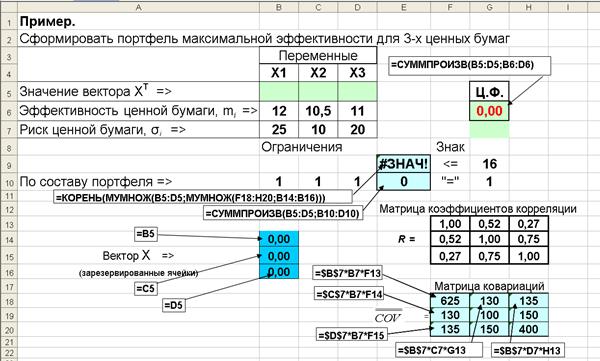
Рис. 4.10.Фрагмент листа Еxcel с исходными данными и расчетными
формулами
В результате решения получена максимально возможная доходность портфеля 11,32 при значениях вектора Х, записанных в ячейки $B5:$D5 (Рис. 4.11.)
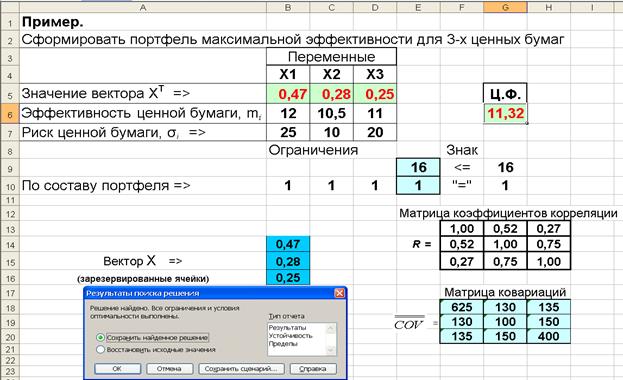
Рис. 4.11.Фрагмент листа Еxcel с результатами расчета оптимального портфеля
Ответ: Максимальную доходность 11,29% можно получить, если доли акций R, S и L составят 0,47, 0,28 и 0,25.
Дата добавления: 2015-05-28; просмотров: 4808;
