Критерии выбора решений в условиях частичной неопределенности

Рассмотренные ранее ситуации максимизации среднего ожидаемого дохода (3.2) и минимизации среднего ожидаемого риска (3.6) с известной вероятностью p_j того, что реальная ситуация развивается по варианту j называются частичной неопределенностью. К этим же случаям можно добавить и критерий Лапласа.

Критерий рациональности Лаплпаса (равновозможности, безразличия) основан на принципе равных вероятностей(p_j = 1/n) для всех вариантов реальной ситуации.

При использовании критерия максимизации среднего ожидаемого дохода 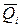выбирается решение, при котором достигается

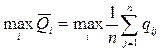, (3.7)

где q_ij – ожидаемый доход при выборе i-го варианта решения и j-ом состоянии среды (ситуации).

В случае минимизации среднего ожидаемого риска 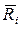выбирается вариант решения, для которого обеспечивается

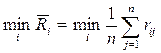. (3.8)

r _ij – ожидаемые потери при выборе i-го решенияварианта и реализации j-го варианта состоянии среды.

Пример 3.2. Используя критерий Лапласа равновозможности для исходных данных, приведенных в матрице последствий

,

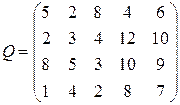необходимо выбрать наилучший вариант решения на основе: а) правила максимизации среднего ожидаемого дохода; б) правила минимизации среднего ожидаемого риска.

Решение.

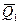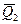а) С учетом равной вероятности пяти вариантов исходов реальной ситуации (p_j =1/n=1/5), значения среднего ожидаемого дохода для каждого из вариантов решения оцениваются по выражению (3.2) и составляют =5, = 6,2, 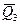= 7,00, 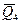= 4,4 (рис.3.7).

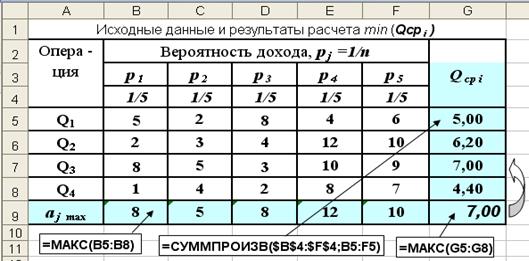
Рис. 3.7. Результаты расчета среднего ожидаемого дохода

Согласно критерию Лапласа (3.7), наилучшим вариантом решения будет третий, с максимальным средним ожидаемым доходом равным 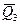=7,00.

б) Рассчитываются элементы матрицы рисков по выражению (3.4) и для каждого варианта решения по выражению (3.6) вычисляются значения среднего ожидаемого риска с учетом равновероятности вариантов ситуации: 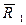= 3,60, 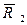= 2,40, 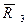= 1,60, 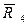= 4,20 (рис.3.8).

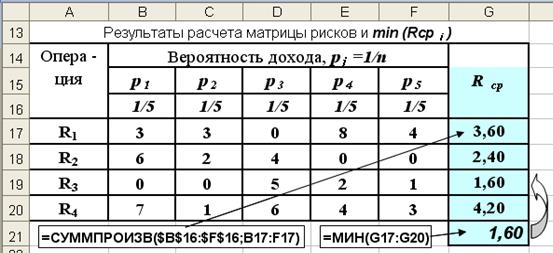
Рис. 3.8. Матрица рисков и величины среднего ожидаемого риска

С учетом критреия Лапласа (3.8) наилучшим будет третий вариант, с минимальным значением среднего ожидаемого риска равным 1,60.