Статистические показатели риска

Хотя статистические показатели по информативности уступают вероятностным, но они широко используются для оценивания уровня риска. Группу статистических показателей оценки риска составляют:

- среднее значение (математическое ожидание)ожидаемого результата деятельности (математическое ожидание);

- разброс (колеблемость) возможного результата деятельности относительно среднего значения.

Среднее значение ожидаемого результата деятельности (или финансовой операции [3]) для дискретных величин определяется средневзвешенным из всех возможных значений результата x_i и вероятностей их появления p_i:

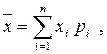(2.20)

где n – число наблюдений.

Если появление всех значений x_i в выборке равновероятно, то рассчитывается выборочная средняя:

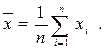(2.21)

Средняя арифметическая 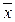= a определяет положение центра распределения кривой нормального распределения, рис. 2.25а.

a) б)

Рис. 2.25. Влияние статистических показателей на положение и форму кривой нормального распределения: а) влияние средней арифметической, б) влияние среднего квадратического отклонения

Изменение a при неизменных остальных условиях (постоянстве σ) приводит к смешению кривой вдоль оси абсцисс без изменения ее формы.

В среде Excel для вычисления 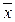используется функция СРЗНАЧ(число1;число2;...).

Пример 2.8. Оценить среднее значение доходности вложения капитала для двух вариантов. Исходные данные приведены на рис. 2.26.

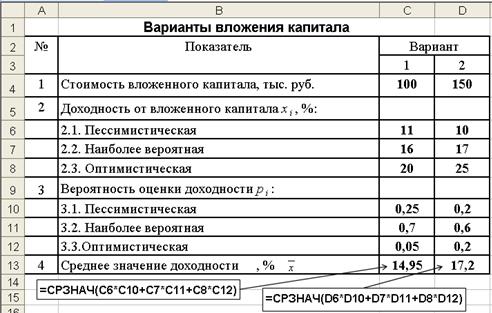
Рис. 2.26. Исходные данные и результаты расчета средней доходности по формуле (2.6)

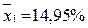Сравнение доходностей двух вариантов вложений капитала (2.7) показывает, что второй вариант более предпочтителен, поскольку для него средняя величина превышает значение . Но такое сравнение не позволяет сделать окончательный выбор, поскольку оно не учитывает степень риска конкретного вложения, которая характеризуется колеблемостью результата относительно среднего значения.

Разброс (колеблемость) возможного результата деятельности относительно среднего значения оценивается показателями вариации (абсолютными или относительными).

К показателям вариации относятся: размах вариации, дисперсия, среднее квадратическое отклонение, доверительный интервал, коэффициент вариации.

1. Размах вариации ожидаемого результата – простейший абсолютный статистический показатель разброса. Рассчитывается как разность:

R = x_max - x_min , (2.22)

где x_max , x_min – наибольшее и наименьшее значение результата в выборке, соответственно.

Большему размаху вариации соответствует больший риск. Поскольку данный показатель учитывает только крайние значения, то он применяется для достаточно однородных совокупностей.

2. Дисперсия (для дискретных случайных величин) – средневзвешенная величина из квадратных отклонений действительных результатов от средних ожидаемых:

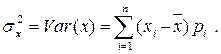(2.23)

Для равновероятных значений дисперсия для генеральной совокупности рассчитывается по формуле

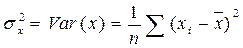. (2.24)

Вычисление дисперсии по последнему выражению можно произвести в среде Excel с помощью функции ДИСПР(число1; число2;…) в категории Статистические.

Выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Предпочтительнее использовать несмещенную оценку дисперсии , которая рассчитывается по формуле .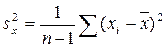

Для вычисления выборочной дисперсии в среде Excel имеется функция ДИСП(число1; число2;…).

3. Среднее квадратическое отклонение является именованной мерой колеблемости (разброса) данных относительно их среднего значения.

Для оценки стандартного (среднего квадратического) отклонения по генеральной совокупности используются следующие формулы:

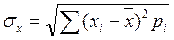, (2.25)

и для равновероятных значений 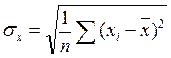. (2.26)

Последнее выражение реализовано в статистической функции Excel СТАНДОТКЛОНП(число1; число2;…).

Оценка стандартного отклонения по выборке для несмещенной оценки производится по выражению 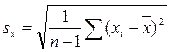, здесь применяется функция СТАНДОТКЛОН(число1; число2;…) – по выборке.

Влияние значения σ_x при неизменном значении средней арифметической 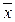на форму кривой нормального распределения приведено на рис. 2.25б. Из рисунка видно, что с увеличением σ при неизменной а кривая становится более пологой, а с уменьшением σ – более крутой.

4. Доверительный интервал – интервал, ограниченный нижним и верхним доверительными пределами, в котором с заданной вероятностью р располагаются возможные значения результата (см. рис. 2.22). Доверительный интервал рассчитывается по известным значениям выборочного среднего ожидаемого значения 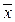и его колеблемости σ_x. Для этой цели может использоваться функция Excel ДОВЕРИТ(альфа;станд_откл;размер), которая рассчитывает значение предельной ошибки выборки D 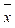= t m_x . Здесь t – коэффициент доверия, m_x – средняя ошибка выборки.

Поскольку выборочное среднее 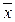является серединой этого диапазона, то доверительный интервал определяется как ( 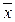± ДОВЕРИТ). Например, если 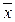– это среднее выборочное значение времени доставки товаров, то математическое ожидание генеральной совокупности принадлежит интервалу ( 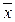± ДОВЕРИТ). Функция ДОВЕРИТ возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности. Способ построения доверительного интервала для математического ожидания зависит от того, известно ли значение дисперсии σ_x².

5. Коэффициента вариации – отношение среднего квадратического отклонения к среднему ожидаемому значению, которое показывает степень отклонения полученных значений. Данный коэффициент выражает количество риска приходящегося на единицу среднего дохода:

k v = 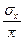. (2.27)

Принято считать: если k _v < 10 %, то колеблемость слабая; если 10 - 25 %, то умеренная и если > 25%, то колеблемость высокая.

По коэффициенту вариации судят об однородности исследуемой совокупности, если k _v < 33%, то совокупность считается однородной.

Принятие решений в условиях риска чаще всего основывается на одном из следующих критериев:

1) ожидаемого значения 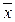(доходности, прибыли или расходов).

2) выборочной дисперсииσ_x² или стандартного (среднего квадратического) отклоненияσ_x.

3) комбинации ожидаемого значения 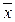идисперсииσ_x² или среднего квадратического отклонения выборки σ_x.

Тема 3. Количественные характеристики и схемы оценки рисков

в условиях неопределенности

3.1. Матрица последствий и матрица рисков

В рисковой ситуации из-за отсутствия необходимой информации результаты деятельности предприятия невозможно представить вероятностными моделями. Такая неопределенность обычно вызывается действием внешних факторов, именуемых «природа».

Процедура принятия решения в данных условиях рассматривается как «игра» между субъектом «игрок 1» (лицо принимающее решение, в дальнейшем ЛПР), который при выборе рискового решения действует сознательно и природой (среда предпринимательства) «игрок 2», который сознательно против «игрока 1» не действует, а выступает как партнер по игре.

Математические модели выбора при принятии решений в условиях неопределенности строятся на основе теории игр.

Выбор решений в условиях неопределенности включает:

- построение платежной матрицы (эффектов) и матрицы риска (ущерба или упущенных возможностей);

- количественную оценку вариантов.

Исходной информацией для принятия решений является платежная матрица (матрица последствий, матрица игры с природой).

Платежная матрица - статистический метод принятия решения на основе выбора наилучшего варианта из нескольких альтернатив по заранее выбранным критериям.

Матрица вида 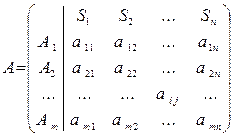, (3.1.)

называется платежной. Здесь A_i – вариант i-го решения(i=1,..,m), S_j – ситуация или состояние среды (j=1,..,n), a_{i j} – ожидаемый выигрыш субъекта при выборе i-го варианта решения и j-ом состоянии среды (ситуации).

Элементы a_ij платежной матрицы отражают оценку последствий (платежи) при различных вариантах действий. Значения a_{i j} могут быть как положительными (оценивают эффект), так и отрицательными (оценивают ущерб).

Платеж представляет собой вознаграждение (полезность), полученное вследствие выбора конкретной стратегии A_i с учетом конкретных обстоятельств S_j .

Платежная матрица обычно используется в следующих случаях:

1) когда ограничено число альтернатив или вариантов стратегии;

2) при отсутствии полной определенности в исходе выбранного варианта решения;

3) когда результаты принятого решения зависят от выбора альтернативы и обстоятельств, которые в действительности имеют место.

Необходимые расчеты по выбору оптимального решения удобно вести в среде Excel. Общий вид платежной матрицы с дополнительной строкой и двумя столбцами, в которые заносятся наибольшие a _{j max}, a _{i max} и наименьшее a _{i min} значения выигрышей, представлен на рис. 3.1.

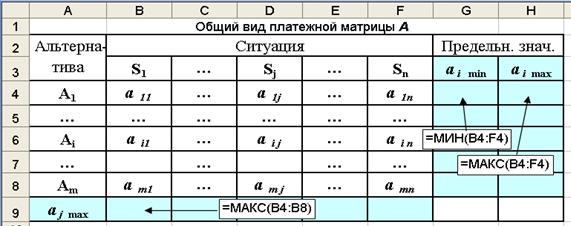
Рис. 3.1. Макет платежной матрицы в Excel

Каждая строка матрицы соответствует одному из вариантов альтернативных решений A_i, а каждый столбец - одной из возможных ситуаций S_j, которые могут возникнуть при разных значениях отсутствующей у ЛПР информации об условиях решения проблемы или об ожидаемых результатах.

Задача игрока сводится к выбору такого варианта, который бы обеспечил наибольшую выгоду по сравнению с другими.

Дополнительно к этому ЛПР должно располагать возможностью объективной оценки вероятности релевантных событий (для которых получаемый результат соответствует желаемому) и расчета ожидаемого значения такой вероятности. Ситуации полной определенности (вероятность p – близка к 1,0), либо полной неопределенности (вероятность близка к нулю) проявляются редко. Поэтому ЛПР во многих случаях приходится самостоятельно оценивать вероятность или возможность появления j-го события (условия частичной неопределенности, когда 0<p<1,0) на основе анализа прошлых тенденций, своей субъективной оценки или собственного опыта действий в подобных ситуациях.

Учет вероятности прямо влияет на определение ожидаемого значения в платежной матрице. Неучет вероятности в расчетах приводит к выбору решения с более оптимистическим последствием.

При количественной оценке альтернативных вариантов возможны два случая.

1-й случай. Вероятности возникновения каждой j-ой ситуации определяются по результатам обработки статистических наблюдений.

Для каждой альтернативы определяется математическое ожидание значения альтернативы или варианта стратегии, которое представляется суммой произведений возможных значений a _{i j} на соответствующие вероятности p _j :

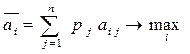. (3.2)

Затем выбирается альтернативный вариант A _i , для которого математическое ожидание выигрыша окажется максимальным, т.е. .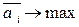

Общий вид платежной матрицы с вероятностями возникновения j-ой ситуации приведен на рис. 3.2.

Рис. 3.2. Макет платежной матрицы с учетом вероятностей

2-й случай. Статистические данные о значениях вероятности p_j отсутствуют, тогда производится экспертная оценка вероятности появления j-ой ситуации.

Экспертам предлагаются три значения ожидаемой величины S _j, характеризующей ситуацию: оптимистическую, пессимистическую и наиболее вероятную (модальную). С помощью таких тройственных оценок приближенно определяется математическое ожидание прогнозируемой величины, т.е. средневероятное значение S ^c_j. При биноминальном распределении можно использовать следующую расчетную формулу:

S ^c_j = 1/6 [( S _j )min + 4( S _j )max]. (3.3)

Исходные данные могут представляться и виде матрицы рисков.

Матрица рисков (матрица упущенных возможностей) − матрица, в строках которой расположены альтернативные варианты рисковых событий, а в столбцах – их вероятности свершения и возможные последствия (ситуации).

Количественной оценкой риска для каждого i-го решения при j-ой ситуации принято считать разницу между максимально возможным для этой ситуации эффектом (a_j )_max и его фактическим значением a _ij :

r _ij = (a_j )_max – a _ij . (3.4)

Тогда матрица рисков записывается в следующем виде:

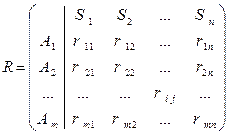, (3.5)

где r _ij – ожидаемые потери субъекта при реализации им i-го решенияварианта A_i (i=1,..,m) при реализации j-го варианта состоянии среды S_j (j=1,..,n).

Оптимальному варианту решения соответствует минимальное математическое ожидание риска:

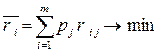, (3.6)

где p_j – вероятность появления j-ой ситуации.

Пример 3.1. По известной платежной матрице (эффектов и ущерба)

S₁ S₂ S₃ S₄ S₅

A₁ 1 2 3 5 5

A₂ 2 0 5 8 7

A₃ 3 4 5 8 7

A₄ 3 3 6 7 5

необходимо построить матрицу рисков и выбрать альтернативное решение без учета данных о вероятности отдельных ситуаций и с учетом ожидаемых значений вероятностей реализации той или иной ситуации р₁=0,10; р₂=0,25; р₃=0,30; р₄=0,15; р₅=0,20.

Решение.

1. Элементы платежной матрицы вводятся в Excel и оформляются в виде таблицы с необходимыми комментариями, рис. 3.3.

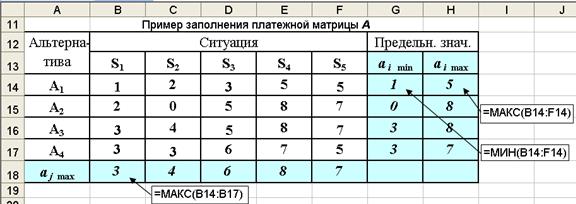
Рис. 3.3. Исходные данные, расчетные формулы и результаты расчета

2. Используя встроенную функцию МАКС вычисляются наибольшие значения элементов матрицы по каждой j-ой ситуации (a_j)_max: (a₁)_max = 3; (a₂)_max = 4; (a₃)_max = 6; (a₄)_max = 8; (a₅)_max = 7, по которым можно установить номера вариантов решений соответствующих максимально возможным значениям эффекта.

Если элементы исходной матрицы характеризуют ущерб, то рассматривается противоположная задача c вычислением минимального размера возможного ущерба (функция МИН) (a _j)_min: (a₁)_min = 1; (a₂)_min = 0; (a₃)_min = 3; (a₄)_min = 5; (a₅)_min = 5 и последующим определением соответствующего номера варианта решения (на рис. 3.3 строка a _{j min} не показана).

Аналогично можно поступить с оценками максимально (a_i)_max или минимально (a_j)_min возможного эффекта (ущерба) по каждому i –му варианту решения при изменении ситуации (см. рис. 3.3, последние два столбца).

3. Рассчитываются оценки риска для каждого i-го решения при j-ой ситуации с использованием выражения (3.4) и заполняется матрица риска, рис. 3.4.

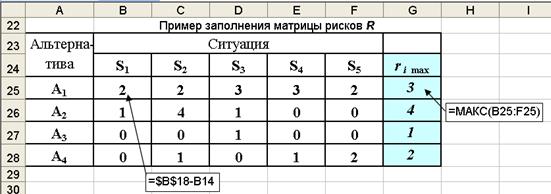
Рис. 3.4. Матрица риска и расчетные формулы

4. Из альтернативных вариантов, можно выбирать оптимальный вариант решения с минимальным значением риска, ему соответствует вариант А3.

5. По выражению (3.6) производится расчет риска операций с учетом вероятности появления j-ой ситуации и заполняется графа Риск, рис.3.5.

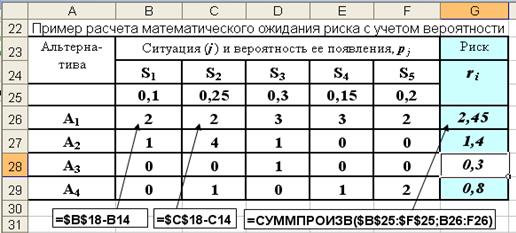
Рис. 3.5. Результаты оценки рисков альтернативных вариантов

По результатам расчета (ячейки G26:G29) выбирается оптимальный вариант А₃, с минимальным математическим ожиданием риска равным 0,3.