Вероятностные показатели риска

Поскольку риск рассматривается как вероятностная категория, то его мерой может быть вероятность, величина которой определяется действием внешних и внутренних фактов. Тогда для количественной оценки риска могут использоваться методы теории вероятностей и математической статистики. Исходная информация о рисковой ситуации представляется в виде частот появления рискового события.

Точечная оценка показателя риска.Показателем оценки риска R является вероятность получения фактического результата меньше требуемого (желаемого, планируемого, прогнозируемого) значения. Данное условие записывается в следующем виде:

R = p ( X < D_тр ) , (2.14)

где R – показатель (функция распределения) оценки риска;

p – вероятность риска,

X – текущее значение результата как случайной величины (ПР).

D_тр– требуемое (желаемое, планируемое, прогнозируемое) значение результата.

Показатель R используется в тех случаях, когда определен тип и параметры закона распределения. Закон распределения дает наиболее полную характеристику степени риска. Обычно в экономических исследованиях принимается нормальный закон распределения. Кривая распределения вероятностей получения прибыли (рис. 2.16) строится при определенных предположениях:

1. Наиболее вероятно получение прибыли, равной расчетной величине – ПРр, вероятность (Вр) получения такой прибыли максимальна. Поэтому значение ПРр считатют математическим ожиданием прибыли. Чем больше прибыль отличается от расчетной, тем ниже вероятность ее получения, т. е. значения вероятностей отклонения от расчетной прибыли монотонно убывают при росте отклонений.

2. Потерями прибыли (DПР) считается ее уменьшение в сравнении с расчетной величиной ПРр. Если реальная прибыль равна ПР, то потери будут определяться разностью DПР = ПРр - ПР. Потери имеют место, когда DПР > 0, в противном случае при DПР < 0 имеет место выигрыш.

3. Вероятность исключительно больших потерь практически равна нулю, поскольку они заведомо имеют верхний предел (исключая потери, которые не возможно оценить количественно).

Хотя принятые допущения соблюдаются не для всех видов риска, но они верно отражают общие закономерности изменения риска и базируются на гипотезе, что прибыль как случайная величина подчинена нормальному или близкому к нормальному закону распределения.

Рис. 2.16. Кривая плотности нормального распределения (вероятностей получения) прибыли определенного уровня

Уравнение для плотности нормального распределения имеет следующий вид

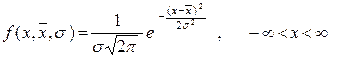. (2.15)

Здесь 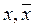- случайная величина и ее среднее арифметическое значение, соответственно; σ – среднее квадратическое отклонение x.

В Excel используется функция НОРМРАСП(x;среднее;стандартное_ откл;интегральная), которая возвращает нормальную функцию распределения для выбранного среднего и стандартного отклонения. Здесь аргументами функции являются: x – значение, для которого строится распределение; среднее – среднее арифметическое распределения; стандартное_ откл – стандартное отклонение распределения, интегральная – логическое значение. Если аргумент интегральнаяпринимает значение ЛОЖЬ или 0, то функция НОРМРАСП вычисляет значение плотности вероятности по выражению (2.15) для заданного значения x при известном математическом ожидании и среднем квадратическом отклонении. Задаваясь интервалом изменения случайной величины x, можно построить всю кривую плотности распределения, либо ее фрагмент.

Уравнение нормальной функции распределения

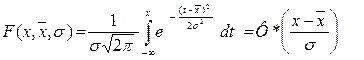(2.16)

позволяет вычислять вероятности того, что случайная величина не превысит заданного уровня. По этому же уравнению можно построить график функции нормального распределения. Алгоритм вычислений с использованием данной функции реализован в Excel НОРМРАСП(x;среднее; стандартное_откл; интегральная), но в ней аргумент интегральная принимает значение ИСТИНА или 1.

На рис. 2.16. заштрихованная площадь под кривой распределения соответствует вероятности получения гарантированного результата не ниже требуемого D_тр. Выражение для расчета показателя риска R (применительно к заштрихованной области) приведено на этом же рисунке.

Пример 2.5.Пусть ожидаемый доход по одному активу имеет распределение со средним значением 20% и стандартным отклонением 30%. Текущая цена актива составляет 100 млн. долл. Необходимо (используя средства Excel) для данных условий на конец года выполнить следующее:

1. Рассчитать и построить график функции плотности нормального распределения f(x) в диапазоне от 0 до 240 млн. долл.

2. Рассчитать и построить график функции распределения F(x) на интервале от 0 до 240 млн. долл.

3. Оценить вероятность понести убыток к концу года более 20 млн. долл. (т.е. вероятность того, что цена актива окажется ниже 80 млн. долл.).

4. Вычислить значение плотности вероятности для значения 80 млн. долл.

5. Вычислить вероятность того, что значение по заданной вероятности 0,90 больше остальных значений нормального распределения.

6. Оценить с вероятностью 1% возможный максимальный убыток к концу года. (Стоимость подверженнаую риску (VaR) с вероятностью 1%).