Центральные интерполяционные формулы

Наряду с приведенными формулами имеются еще так называемые центральные интерполяционные формулы, рассчитанные на применение в центральной части таблицы.

Пусть 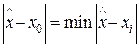, при i=1,2,…,n , таким образом в этом случае базовым узлом будет 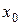, и будем строить интерполяционный многочлен в форме

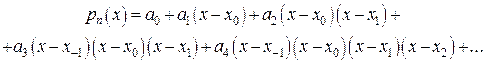(33)

т.е. последовательно подключая узлы сначала снизу, а потом сверху. Так же, как и в предыдущих случаях, для определения коэффициентов разложения 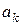будем последовательно подставлять значения 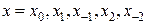и получим:

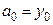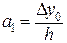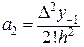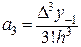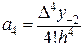; ; ; ; (34)

Подставляя в исходное выражение (33) и аналогично вводя переменную 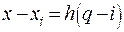, приходим к первой интерполяционной формуле Гаусса:

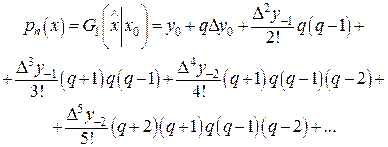(35)

Изменяя порядок подключения узлов (сначала сверху, затем снизу и т.д. в последовательности 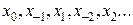) и определяя коэффициенты разложения, получаем вторую интерполяционную формулу Гаусса

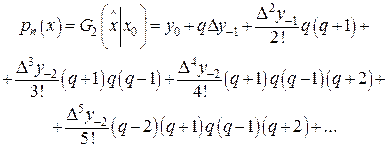(36)

Из (35) и (36) можно получить удобные формулы, использующие центральные разности. Так, полусумма первой и второй формулы приводит к соотношению

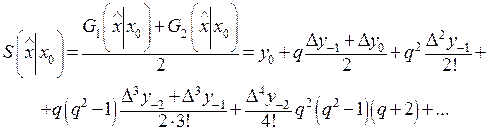(37)

называемому интерполяционной формулой Стирлинга.

Преобразуем (33), взяв в качестве базового узла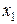

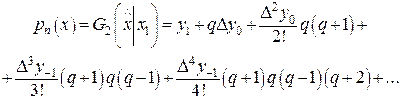
Взяв полусумму,

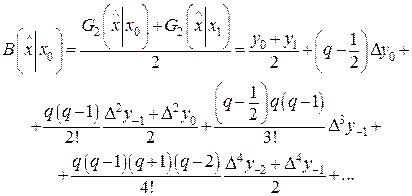(38)

получаем интерполяционную формулу Бесселя.

На диагональной таблице разностей (стр.14) направления интерполяции в форме Стирлинга и Бесселя показаны соответственно пунктирной и штриховой стрелками. Вертикальными стрелками отмечены полусуммы значений функции и разностей.